【题目】如图,椭圆![]() 的离心率为
的离心率为![]() ,顶点为
,顶点为![]() ,且
,且![]() .
.
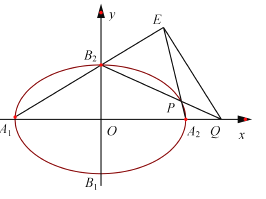
(1)求椭圆![]() 的方程;
的方程;
(2)![]() 是椭圆
是椭圆![]() 上除顶点外的任意点,直线
上除顶点外的任意点,直线![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .设
.设![]() 的斜率为
的斜率为![]() ,
, ![]() 的斜率为
的斜率为![]() ,试问
,试问![]() 是否为定值?并说明理由.
是否为定值?并说明理由.
参考答案:
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:(1)因为![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() ,即可求解
,即可求解![]() 的值,得出椭圆的方程;
的值,得出椭圆的方程;
(2)由题意可知直线![]() 的方程为
的方程为![]() 与椭圆的方程联立方程组,求得
与椭圆的方程联立方程组,求得![]() 点的坐标,进而得到点
点的坐标,进而得到点![]() 的坐标,在根据直线
的坐标,在根据直线![]() 的方程与
的方程与![]() 联立,得到点
联立,得到点![]() 的坐标,即可表示
的坐标,即可表示![]() 的斜率,得出结论.
的斜率,得出结论.
试题解析:(1)因为![]() ,所以
,所以![]() ,
,
由题意及图可得![]() ,
,
所以![]()
又![]() ,所以
,所以![]() ,所以
,所以![]()
所以![]()
所以椭圆![]() 的方程为:
的方程为: ![]()
(2)证明:由题意可知![]() ,
, ![]() ,
, ![]() ,
, ![]()
因为![]() 的斜率为
的斜率为![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]()
由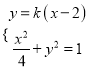 得
得![]()
其中![]() ,所以
,所以![]() ,所以
,所以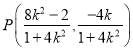
则直线![]() 的方程为
的方程为![]() (
(![]() )
)
令![]() ,则
,则![]() ,即
,即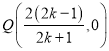
直线![]() 的方程为
的方程为![]() ,
,
由![]() 解得
解得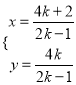 ,所以
,所以![]()
所以![]() 的斜率
的斜率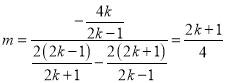
所以![]() (定值)
(定值)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 分别是双曲线E:
分别是双曲线E: 
 的左、右焦点,P是双曲线上一点,
的左、右焦点,P是双曲线上一点,  到左顶点的距离等于它到渐近线距离的2倍,(1)求双曲线的渐近线方程;(2)当
到左顶点的距离等于它到渐近线距离的2倍,(1)求双曲线的渐近线方程;(2)当 时,
时,  的面积为
的面积为 ,求此双曲线的方程。
,求此双曲线的方程。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,五面体
 中,四边形
中,四边形 是菱形,
是菱形, 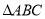 是边长为2的正三角形,
是边长为2的正三角形, 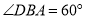 ,
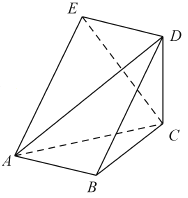
, 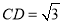 .
.
(1)证明:
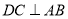 ;
;(2)若点
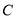 在平面
在平面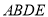 内的射影
内的射影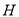 ,求
,求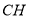 与平面
与平面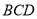 所成的角的正弦值.
所成的角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数f1(x)、f2(x)、h(x),如果存在实数a,b使得h(x)=af1(x)+bf2(x),那么称h(x)为f1(x)、f2(x)的和谐函数.
(1)已知函数f1(x)=x﹣1,f2(x)=3x+1,h(x)=2x+2,试判断h(x)是否为f1(x)、f2(x)的和谐函数?并说明理由;
(2)已知h(x)为函数f1(x)=log3x,f2(x)=log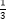 x的和谐函数,其中a=2,b=1,若方程h(9x)+th(3x)=0在x∈[3,9]上有解,求实数t的取值范围.
x的和谐函数,其中a=2,b=1,若方程h(9x)+th(3x)=0在x∈[3,9]上有解,求实数t的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
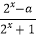 ,(a>0).
,(a>0).
(1)当a=2时,证明函数f(x)不是奇函数;
(2)判断函数f(x)的单调性,并利用函数单调性的定义给出证明;
(3)若f(x)是奇函数,且f(x)﹣x2+4x≥m在x∈[﹣2,2]时恒成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方体
 中,E、F分别是
中,E、F分别是 、CD的中点,(1)证明:
、CD的中点,(1)证明: 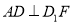 ;(2)求异面直线
;(2)求异面直线 与
与 所成的角;(3)证明:平面
所成的角;(3)证明:平面 平面
平面 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图椭圆
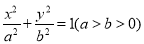 的上下顶点为A、B,直线
的上下顶点为A、B,直线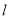 :
: 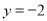 ,点P是椭圆上异于点A、B的任意一点,连结AP并延长交直线
,点P是椭圆上异于点A、B的任意一点,连结AP并延长交直线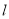 于点N,连结BP并延长交直线
于点N,连结BP并延长交直线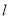 于点M,设AP、BP所在直线的斜率分别为
于点M,设AP、BP所在直线的斜率分别为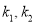 ,若椭圆的离心率为
,若椭圆的离心率为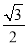 ,且过点
,且过点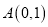 ,(1)求
,(1)求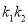 的值,并求
的值,并求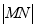 最小值;(2)随着点P的变化,以MN为直径的圆是否恒过定点,若过定点,求出该定点坐标;若不过定点,请说明理由。
最小值;(2)随着点P的变化,以MN为直径的圆是否恒过定点,若过定点,求出该定点坐标;若不过定点,请说明理由。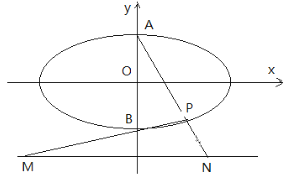
相关试题

