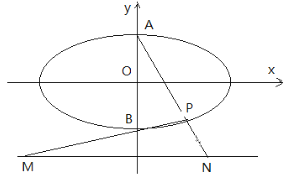
【题目】如图椭圆![]() 的上下顶点为A、B,直线
的上下顶点为A、B,直线![]() :
: ![]() ,点P是椭圆上异于点A、B的任意一点,连结AP并延长交直线
,点P是椭圆上异于点A、B的任意一点,连结AP并延长交直线![]() 于点N,连结BP并延长交直线
于点N,连结BP并延长交直线![]() 于点M,设AP、BP所在直线的斜率分别为
于点M,设AP、BP所在直线的斜率分别为![]() ,若椭圆的离心率为
,若椭圆的离心率为![]() ,且过点
,且过点![]() ,(1)求
,(1)求![]() 的值,并求
的值,并求![]() 最小值;(2)随着点P的变化,以MN为直径的圆是否恒过定点,若过定点,求出该定点坐标;若不过定点,请说明理由。
最小值;(2)随着点P的变化,以MN为直径的圆是否恒过定点,若过定点,求出该定点坐标;若不过定点,请说明理由。
参考答案:
【答案】(1)![]() ,
, ![]() 的最小值为
的最小值为![]() (2)
(2)![]()
【解析】试题分析:(1)由题意可知![]() ,又
,又![]() ,解出
,解出![]() 得到椭圆方程,设椭圆上点
得到椭圆方程,设椭圆上点![]() ,代入椭圆方程,再由斜率公式,即可得到
,代入椭圆方程,再由斜率公式,即可得到![]() 的值,设
的值,设![]() ,求出
,求出![]() ,再由基本不等式求出
,再由基本不等式求出![]() 的最小值;(2)设
的最小值;(2)设![]() ,则以
,则以![]() 为直径的圆的方程为
为直径的圆的方程为![]() ,化简整理,若圆过定点,则有
,化简整理,若圆过定点,则有![]() ,化简整理,若圆过定点,则有
,化简整理,若圆过定点,则有![]() ,解出即可判断.
,解出即可判断.
试题解析:(1)因为![]() ,所以此椭圆的方程是
,所以此椭圆的方程是![]() ;
;
设点P的坐标为![]() ,有
,有![]() ,所以
,所以![]() ,
,
设![]() ,则
,则![]() ,可得
,可得![]() ;
;
不妨设![]() ,则
,则![]() ,所以当且仅当
,所以当且仅当![]() 时,
时, ![]() 的最小值为
的最小值为![]() ;
;
(2)因为![]() ,则以M、N为直径的圆的方程为
,则以M、N为直径的圆的方程为![]() ,即
,即![]() ,因圆过定点,则有
,因圆过定点,则有![]() ,解得
,解得![]() ,即定点为
,即定点为![]() .
.
-
科目: 来源: 题型:
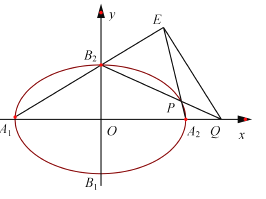
查看答案和解析>>【题目】如图,椭圆
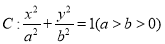 的离心率为
的离心率为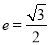 ,顶点为
,顶点为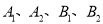 ,且
,且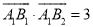 .
.
(1)求椭圆
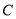 的方程;
的方程;(2)
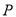 是椭圆
是椭圆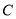 上除顶点外的任意点,直线
上除顶点外的任意点,直线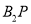 交
交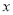 轴于点
轴于点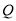 ,直线
,直线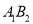 交
交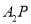 于点
于点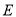 .设
.设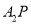 的斜率为
的斜率为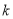 ,
, 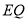 的斜率为
的斜率为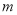 ,试问
,试问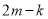 是否为定值?并说明理由.
是否为定值?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
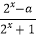 ,(a>0).
,(a>0).
(1)当a=2时,证明函数f(x)不是奇函数;
(2)判断函数f(x)的单调性,并利用函数单调性的定义给出证明;
(3)若f(x)是奇函数,且f(x)﹣x2+4x≥m在x∈[﹣2,2]时恒成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方体
 中,E、F分别是
中,E、F分别是 、CD的中点,(1)证明:
、CD的中点,(1)证明: 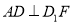 ;(2)求异面直线
;(2)求异面直线 与
与 所成的角;(3)证明:平面
所成的角;(3)证明:平面 平面
平面 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个边长为
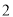 的正三角形和半圆组成的图形,现把
的正三角形和半圆组成的图形,现把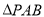 沿直线AB折起使得与圆所在平面垂直,已知点C是半圆的一个三等分点(靠左边一点),点E是线段PB上的点,(1)当点E是PB的中点时,在圆弧上找一点Q,使得
沿直线AB折起使得与圆所在平面垂直,已知点C是半圆的一个三等分点(靠左边一点),点E是线段PB上的点,(1)当点E是PB的中点时,在圆弧上找一点Q,使得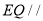 平面
平面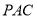 ;(2)当二面角
;(2)当二面角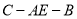 的正切值为
的正切值为 时,求BE的长。
时,求BE的长。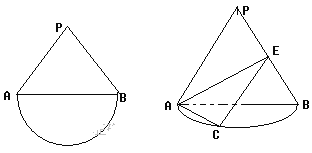
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,  (
( 为自然对数的底数).
为自然对数的底数).(1)讨论函数
 的单调性;
的单调性;(2)当
 时,
时,  恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
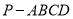 中,底面
中,底面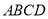 是直角梯形,
是直角梯形, 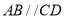 ,
, 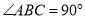 ,
, 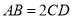 ,
, 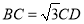 ,
, 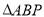 是等边三角形,且侧面
是等边三角形,且侧面 底面
底面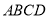 ,
, 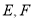 分别是
分别是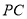 ,
, 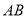 的中点.
的中点.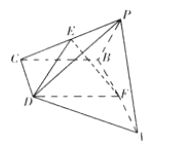
(Ⅰ)求证:
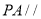 平面
平面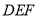 ;
;(Ⅱ)求平面
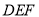 与平面
与平面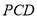 所成的二面角(锐角)的余弦值.
所成的二面角(锐角)的余弦值.
相关试题

