【题目】已知命题p:实数x满足x2-5ax+4a2<0,其中a>0,命题q:实数x满足![]() .
.
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)命题p:实数x满足x2-5ax+4a2<0,解集A=(a,4a).命题q:实数x满足![]() 解集B=(2,4].a=1,且p∧q为真,求A∩B即可得出.
解集B=(2,4].a=1,且p∧q为真,求A∩B即可得出.
(2)¬p:(-∞,a]∪[4a,+∞).¬q:(-∞,2]∪(4,+∞).利用¬p是¬q的充分不必要条件,即可得出.
试题解析:
(1)命题p:实数x满足x2-5ax+4a2<0,其中a>0,a<x<4a,解集A=(a,4a),命题q:实数x满足![]() ,解得2<x≤4.解集B=(2,4],a=1,且p∧q为真,则A∩B=(1,4)∩(2,4]=(2,4),∴实数x的取值范围是(2,4).
,解得2<x≤4.解集B=(2,4],a=1,且p∧q为真,则A∩B=(1,4)∩(2,4]=(2,4),∴实数x的取值范围是(2,4).
(2)¬p:(-∞,a]∪[4a,+∞),¬q:(-∞,2]∪(4,+∞).
若¬p是¬q的充分不必要条件,则![]() ,解得1≤a≤2.
,解得1≤a≤2.
又当a=1时不成立∴实数a的取值范围是(1,2].
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,斜三棱柱
 中,侧面
中,侧面 为菱形,底面
为菱形,底面 是等腰直角三角形,
是等腰直角三角形,  .
.
(1)求证:直线
 直线
直线 ;
;(2)若直线
 与底面
与底面 成的角为60°,求二面角
成的角为60°,求二面角 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面
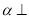 平面
平面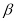 ,
, 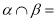 直线
直线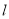 ,
, 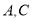 是
是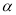 内不同的两点,
内不同的两点, 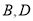 是
是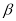 内不同的两点,且
内不同的两点,且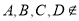 直线
直线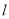 上
上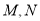 分别是线段
分别是线段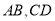 的中点,下列判断正确的是( )
的中点,下列判断正确的是( )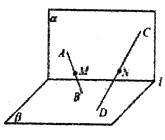
A. 当
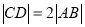 时,
时, 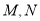 两点不可能重合
两点不可能重合B.
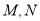 两点可能重合,但此时直线
两点可能重合,但此时直线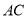 与
与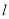 不可能相交
不可能相交C. 当
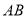 与
与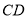 相交,直线
相交,直线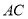 平行于
平行于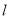 时,直线
时,直线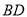 可以与
可以与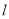 相交
相交D. 当
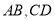 是异面直线时,直线
是异面直线时,直线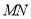 可能与
可能与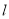 平行
平行 -
科目: 来源: 题型:
查看答案和解析>>【题目】从抛物线y2=32x上各点向x轴作垂线,其垂线段中点的轨迹为E.
(1)求轨迹E的方程;
(2)已知直线l:y=k(x-2)(k>0)与轨迹E交于A,B两点,且点F(2,0),若|AF|=2|BF|,求弦AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组函数中表示同一函数的是( )
①f(x)=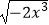 与g(x)=x
与g(x)=x 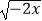
②f(x)=|x|与g(x)=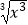
③f(x)=x0与g(x)=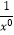
④f(x)=x2﹣2x﹣1与g(t)=t2﹣2t﹣1.
A.①③
B.②③
C.③④
D.①④ -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A,B是抛物线x2=2py(p>0)上的两个动点,O为坐标原点,非零向量
 满足
满足 .
. (1)求证:直线AB经过一定点;
(2)当AB的中点到直线y-2x=0的距离的最小值为
 时,求p的值.
时,求p的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中常数
,其中常数 .
.(1)当
 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;(2)设定义在
 上的函数
上的函数 在点
在点 处的切线方程为
处的切线方程为 ,若
,若 在
在 内恒成立,则称
内恒成立,则称 为函数
为函数 的“类对称点”,当
的“类对称点”,当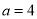 时,试问
时,试问 是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标;若不存在,请说明理由.
是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标;若不存在,请说明理由.
相关试题

