【题目】已知函数![]() ,其中常数
,其中常数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调递增区间;
的单调递增区间;
(2)设定义在![]() 上的函数
上的函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,若
,若![]() 在
在![]() 内恒成立,则称
内恒成立,则称![]() 为函数
为函数![]() 的“类对称点”,当
的“类对称点”,当![]() 时,试问
时,试问![]() 是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标;若不存在,请说明理由.
是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)存在,
;(2)存在, ![]() .
.
【解析】试题分析:(1)先求得定义域![]() 求导得
求导得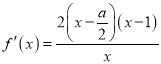 ,由于
,由于![]() ,所以增区间为
,所以增区间为![]() ;(2)当
;(2)当![]() 时,
时, ![]() ,利用导数求得切线
,利用导数求得切线 ,两式相减得
,两式相减得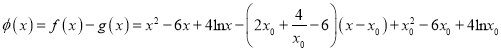 ,利用导数求得以当
,利用导数求得以当![]() 时,
时, ![]() 存在“类对称点”.
存在“类对称点”.
试题解析:
(1)函数![]() 的定义域为
的定义域为![]() ,∵
,∵![]() ,∴
,∴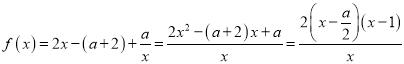 ,∵
,∵![]() ,∴
,∴![]() ,令
,令![]() ,即
,即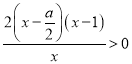 ,∵
,∵![]() ,∴
,∴![]() 或
或![]() ,
,
所以函数![]() 的单调递增区间是
的单调递增区间是![]() ;
;
(2)当![]() 时,
时, ![]() ,
,
∴![]() ,
,  ,
,
令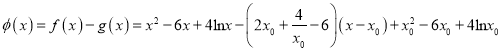 ,
,
则![]() ,
,
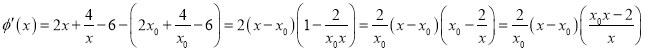 ,当
,当![]() 时,
时, ![]() 在
在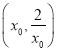 上单调递减.
上单调递减.
∴当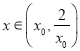 时,
时, ![]() ,
,
从而有 时,
时, ![]() ,
,
当![]() 时,
时, ![]() 在
在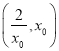 上单调递减,
上单调递减,
∴当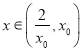 时,
时, ![]() ,
,
从而有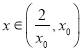 时,
时, ![]() ,
,
∴当![]() 时,
时, ![]() 不存在“类对称点”.
不存在“类对称点”.
当![]() 时,
时, ![]() ,
,
∴![]() 在
在![]() 上是增函数,故
上是增函数,故![]() ,
,
所以当![]() 时,
时, ![]() 存在“类对称点”.
存在“类对称点”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题p:实数x满足x2-5ax+4a2<0,其中a>0,命题q:实数x满足
 .
. (1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组函数中表示同一函数的是( )
①f(x)=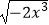 与g(x)=x
与g(x)=x 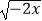
②f(x)=|x|与g(x)=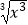
③f(x)=x0与g(x)=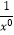
④f(x)=x2﹣2x﹣1与g(t)=t2﹣2t﹣1.
A.①③
B.②③
C.③④
D.①④ -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A,B是抛物线x2=2py(p>0)上的两个动点,O为坐标原点,非零向量
 满足
满足 .
. (1)求证:直线AB经过一定点;
(2)当AB的中点到直线y-2x=0的距离的最小值为
 时,求p的值.
时,求p的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题p:方程
 表示焦点在x轴上的椭圆;命题q:双曲线
表示焦点在x轴上的椭圆;命题q:双曲线 的离心率e∈
的离心率e∈ .若命题“p∨q”为真命题,“p∧q”为假命题,求m的取值范围.
.若命题“p∨q”为真命题,“p∧q”为假命题,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设等差数列
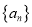 的前
的前 项和为
项和为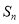 ,已知
,已知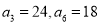 .
.(1)求数列
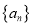 的通项公式;
的通项公式;(2)求数列
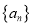 的前
的前 项和为
项和为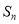 ;
;(3)当
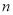 为何值时,
为何值时, 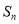 最大,并求
最大,并求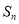 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
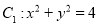 与圆
与圆 ,点
,点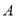 在圆
在圆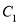 上,点
上,点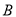 在圆
在圆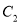 上.
上.(1)求
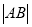 的最小值;
的最小值;(2)直线
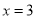 上是否存在点
上是否存在点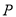 ,满足经过点
,满足经过点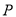 由无数对相互垂直的直线
由无数对相互垂直的直线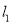 和
和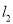 ,它们分别与圆
,它们分别与圆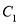 和圆
和圆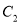 相交,并且直线
相交,并且直线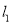 被圆
被圆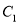 所截得的弦长等于直线
所截得的弦长等于直线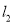 被圆
被圆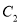 所截得的弦长?若存在,求出点
所截得的弦长?若存在,求出点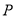 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
相关试题

