【题目】某商场进行有奖促销活动,顾客购物每满500元,可选择返回50元现金或参加一次抽奖,抽奖规则如下:从1个装有6个白球、4个红球的箱子中任摸一球,摸到红球就可获得100元现金奖励,假设顾客抽奖的结果相互独立.
(Ⅰ)若顾客选择参加一次抽奖,求他获得100元现金奖励的概率;
(Ⅱ)某顾客已购物1500元,作为商场经理,是希望顾客直接选择返回150元现金,还是选择参加3次抽奖?说明理由;
(Ⅲ)若顾客参加10次抽奖,则最有可能获得多少现金奖励?
参考答案:
【答案】(Ⅰ)![]() (Ⅱ)希望顾客参加抽奖.(Ⅲ)400
(Ⅱ)希望顾客参加抽奖.(Ⅲ)400
【解析】
试题分析:(Ⅰ)先确定从装有10个球的箱子中任摸一球的结果有10种,其中摸到红球的结果有4种,因此根据古典概型概率求法得![]() (Ⅱ)比较与3次抽奖的数学期望的大小,由于3次抽奖是相互独立,所以可视为独立重复试验,其变量服从二项分布
(Ⅱ)比较与3次抽奖的数学期望的大小,由于3次抽奖是相互独立,所以可视为独立重复试验,其变量服从二项分布![]() ,由此可得数学期望为
,由此可得数学期望为![]() ,即三次抽奖中可获得的奖励金额的均值为
,即三次抽奖中可获得的奖励金额的均值为![]() 元.
元.
(Ⅲ)求概率最大时对应的奖金:由于变量服从二项分布![]() ,所以作商得
,所以作商得![]() ,
,![]() ,因此
,因此![]() 最大,即获得400元的现金
最大,即获得400元的现金
试题解析:(Ⅰ)因为从装有10个球的箱子中任摸一球的结果共有![]() 种,摸到红球的结果共有
种,摸到红球的结果共有![]() 种,所以顾客参加一次抽奖获得100元现金奖励的概率是
种,所以顾客参加一次抽奖获得100元现金奖励的概率是
![]() .……2分
.……2分
(Ⅱ)设![]() 表示顾客在三次抽奖中中奖的次数,由于顾客每次抽奖的结果是相互独立的,则
表示顾客在三次抽奖中中奖的次数,由于顾客每次抽奖的结果是相互独立的,则
![]() ,
,
所以![]() .
.
由于顾客每中奖一次可获得100元现金奖励,因此该顾客在三次抽奖中可获得的奖励金额的
均值为![]() 元.
元.
由于顾客参加三次抽奖获得现金奖励的均值120元小于直接返现的150元,所以商场经理希望顾客参加抽奖.……………7分
(Ⅲ)设顾客参加10次抽奖摸中红球的次数为![]() .
.
由于顾客每次抽奖的结果是相互独立的,则![]() .
.
于是,恰好![]() 次中奖的概率为
次中奖的概率为
![]() ,
,![]() .
.
从而![]() ,
,![]() ,
,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
则![]() 最大.
最大.
所以,最有可能获得的现金奖励为![]() 元.
元.
于是,顾客参加10次抽奖,最有可能获得400元的现金奖励.………………12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
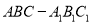 中,底面
中,底面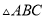 是边长为2的等边三角形,
是边长为2的等边三角形, 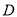 为
为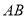 的中点.
的中点.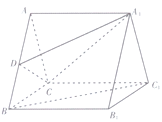
(1)求证:
 平面
平面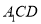 ;
;(2)若四边形
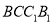 是正方形,且
是正方形,且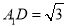 ,求直线
,求直线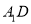 与平面
与平面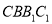 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
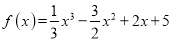 .
.(Ⅰ)求
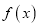 的单调区间;
的单调区间;(Ⅱ)若曲线
 与
与 有三个不同的交点,求实数
有三个不同的交点,求实数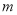 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】2014年3月的“两会”上,李克强总理在政府工作报告中,首次提出“倡导全民阅读”,某学校响应政府倡导,在学生中发起读书热潮.现统计了从2014年下半年以来,学生每半年人均读书量,如下表:
时间
2014年下半年
2015年上半年
2015年下半年
2016年上半年
2016年下半年
时间代号
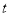
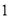
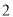
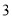
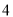
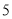
人均读书量
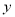 (本)
(本)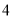
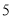
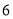
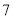
根据散点图,可以判断出人均读书量
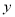 与时间代号
与时间代号 具有线性相关关系.
具有线性相关关系.(1)求
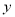 关于
关于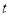 的回归方程
的回归方程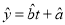 ;
;(2)根据所求的回归方程,预测该校2017年上半年的人均读书量.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
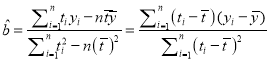 ,
, 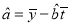
-
科目: 来源: 题型:
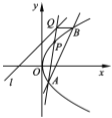
查看答案和解析>>【题目】已知直线
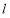 的方程为
的方程为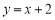 ,点
,点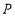 是抛物线
是抛物线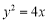 上到直线
上到直线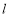 距离最小的点,点
距离最小的点,点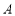 是抛物线上异于点
是抛物线上异于点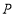 的点,直线
的点,直线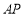 与直线
与直线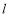 交于点
交于点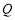 ,过点
,过点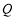 与
与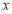 轴平行的直线与抛物线
轴平行的直线与抛物线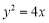 交于点
交于点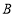 .
.
(Ⅰ)求点
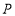 的坐标;
的坐标;(Ⅱ)证明直线
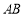 恒过定点,并求这个定点的坐标.
恒过定点,并求这个定点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 ,
,  ,函数
,函数 的图象过点
的图象过点 ,点
,点 与其相邻的最高点的距离为
与其相邻的最高点的距离为 .
.(1)求
 的单调递增区间;
的单调递增区间;(2)计算
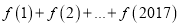 ;
;(3)设函数
 ,试讨论函数
,试讨论函数 在区间
在区间 上的零点个数.
上的零点个数. -
科目: 来源: 题型:
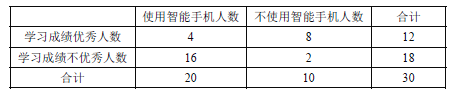
查看答案和解析>>【题目】某研究型学习小组调查研究”中学生使用智能手机对学习的影响”.部分统计数据如下表:
参考数据:

参考公式:
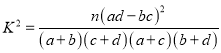 ,其中
,其中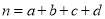
(Ⅰ)试根据以上数据,运用独立性检验思想,指出有多大把握认为中学生使用智能手机对学习有影响?
(Ⅱ)研究小组将该样本中使用智能手机且成绩优秀的4位同学记为
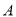 组,不使用智能手机且成绩优秀的8位同学记为
组,不使用智能手机且成绩优秀的8位同学记为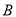 组,计划从
组,计划从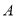 组推选的2人和
组推选的2人和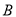 组推选的3人中,随机挑选两人在学校升旗仪式上作“国旗下讲话”分享学习经验.求挑选的两人恰好分别来自
组推选的3人中,随机挑选两人在学校升旗仪式上作“国旗下讲话”分享学习经验.求挑选的两人恰好分别来自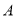 、
、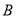 两组的概率.
两组的概率.
相关试题

