【题目】已知向量  ,
, ![]() ,函数
,函数![]() 的图象过点
的图象过点![]() ,点
,点![]() 与其相邻的最高点的距离为
与其相邻的最高点的距离为![]() .
.
(1)求![]() 的单调递增区间;
的单调递增区间;
(2)计算![]() ;
;
(3)设函数![]() ,试讨论函数
,试讨论函数![]() 在区间
在区间![]() 上的零点个数.
上的零点个数.
参考答案:
【答案】(1) ![]() .(2) 2018. (3)当
.(2) 2018. (3)当![]() 或
或![]() 时,函数
时,函数![]() 在
在![]() 上无零点;当
上无零点;当![]() 或
或![]() 时,函数
时,函数![]() 在
在![]() 上有一个零点;当
上有一个零点;当![]() 时,函数
时,函数![]() 在
在![]() 有两个零点.
有两个零点.
【解析】试题分析:(1)根据平面向量数量积的坐标表示、二倍角公式和与辅助角公式可得![]() ,根据
,根据![]() 的图象过点
的图象过点![]() ,点
,点![]() 与其相邻的最高点的距离为
与其相邻的最高点的距离为![]() ,确定
,确定![]() ,从而根据正弦函数的单调性可得结果;(2)根据特殊角的三角函数及周期性可得结果;(3)
,从而根据正弦函数的单调性可得结果;(2)根据特殊角的三角函数及周期性可得结果;(3)![]() ,函数
,函数![]() 在区间
在区间![]() 上的零点个数,即为函数
上的零点个数,即为函数![]() 的图象与直线
的图象与直线![]() 在
在![]() 上的交点个数.在同一直角坐标系内作出这两个函数的图象,几何图形可得结果.
上的交点个数.在同一直角坐标系内作出这两个函数的图象,几何图形可得结果.
试题解析:(1) ![]() 向量
向量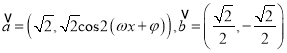 ,
, ![]() ,
, ![]() 点
点![]() 为函数
为函数![]() 图象上的一个最高点,
图象上的一个最高点, ![]() 点
点![]() 与其相邻的最高点的距离为
与其相邻的最高点的距离为![]() ,
, ![]() ,
, ![]() 函数
函数![]() 图象过点
图象过点![]() ,
, ![]() ,
, ![]() ,
, ![]() ,由
,由![]() ,得
,得![]() ,
, ![]() 的单调增区间是
的单调增区间是![]() .
.
(2) 由(1)知![]() 的周期为
的周期为![]() ,且
,且![]() ,
, ![]() ,而
,而![]() .
.
(3) ![]() ,函数
,函数![]() 在区间
在区间![]() 上的零点个数,即为函数
上的零点个数,即为函数![]() 的图象与直线
的图象与直线![]() 在
在![]() 上的交点个数.在同一直角坐标系内作出这两个函数的图象如图所示,
上的交点个数.在同一直角坐标系内作出这两个函数的图象如图所示,

由图象可知,①当![]() 或
或![]() 时,函数
时,函数![]() 的图象与直线
的图象与直线![]() 在
在![]() 上的无公共点,即函数
上的无公共点,即函数![]() 无零点;②当
无零点;②当![]() 与
与![]() 时,函数
时,函数![]() 的图象与直线
的图象与直线![]() 在
在![]() 上有一个公共点,即函数
上有一个公共点,即函数![]() 有一个零点;③当
有一个零点;③当![]() 时,函数
时,函数![]() 的图象与直线
的图象与直线![]() 在
在![]() 上有两个公共点,即函数
上有两个公共点,即函数![]() 有两个零点,综上,当
有两个零点,综上,当![]() 或
或![]() 时,函数
时,函数![]() 在
在![]() 上无零点;当
上无零点;当![]() 或
或![]() 时,函数
时,函数![]() 在
在![]() 上有一个零点;当
上有一个零点;当![]() 时,函数
时,函数![]() 在
在![]() 有两个零点.
有两个零点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2014年3月的“两会”上,李克强总理在政府工作报告中,首次提出“倡导全民阅读”,某学校响应政府倡导,在学生中发起读书热潮.现统计了从2014年下半年以来,学生每半年人均读书量,如下表:
时间
2014年下半年
2015年上半年
2015年下半年
2016年上半年
2016年下半年
时间代号
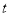
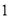
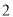
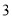
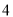
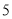
人均读书量
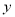 (本)
(本)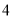
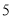
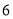
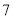
根据散点图,可以判断出人均读书量
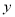 与时间代号
与时间代号 具有线性相关关系.
具有线性相关关系.(1)求
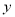 关于
关于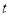 的回归方程
的回归方程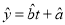 ;
;(2)根据所求的回归方程,预测该校2017年上半年的人均读书量.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
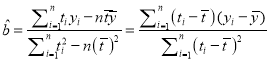 ,
, 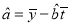
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场进行有奖促销活动,顾客购物每满500元,可选择返回50元现金或参加一次抽奖,抽奖规则如下:从1个装有6个白球、4个红球的箱子中任摸一球,摸到红球就可获得100元现金奖励,假设顾客抽奖的结果相互独立.
(Ⅰ)若顾客选择参加一次抽奖,求他获得100元现金奖励的概率;
(Ⅱ)某顾客已购物1500元,作为商场经理,是希望顾客直接选择返回150元现金,还是选择参加3次抽奖?说明理由;
(Ⅲ)若顾客参加10次抽奖,则最有可能获得多少现金奖励?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
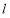 的方程为
的方程为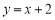 ,点
,点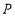 是抛物线
是抛物线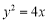 上到直线
上到直线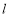 距离最小的点,点
距离最小的点,点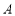 是抛物线上异于点
是抛物线上异于点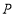 的点,直线
的点,直线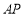 与直线
与直线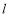 交于点
交于点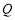 ,过点
,过点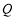 与
与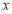 轴平行的直线与抛物线
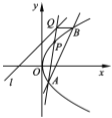
轴平行的直线与抛物线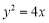 交于点
交于点 .
.
(Ⅰ)求点
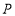 的坐标;
的坐标;(Ⅱ)证明直线
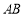 恒过定点,并求这个定点的坐标.
恒过定点,并求这个定点的坐标. -
科目: 来源: 题型:
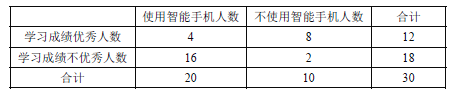
查看答案和解析>>【题目】某研究型学习小组调查研究”中学生使用智能手机对学习的影响”.部分统计数据如下表:
参考数据:

参考公式:
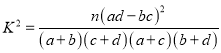 ,其中
,其中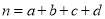
(Ⅰ)试根据以上数据,运用独立性检验思想,指出有多大把握认为中学生使用智能手机对学习有影响?
(Ⅱ)研究小组将该样本中使用智能手机且成绩优秀的4位同学记为
 组,不使用智能手机且成绩优秀的8位同学记为
组,不使用智能手机且成绩优秀的8位同学记为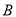 组,计划从
组,计划从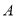 组推选的2人和
组推选的2人和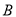 组推选的3人中,随机挑选两人在学校升旗仪式上作“国旗下讲话”分享学习经验.求挑选的两人恰好分别来自
组推选的3人中,随机挑选两人在学校升旗仪式上作“国旗下讲话”分享学习经验.求挑选的两人恰好分别来自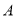 、
、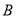 两组的概率.
两组的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
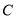 的两个焦点坐标分别是
的两个焦点坐标分别是 ,并且经过
,并且经过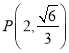 .
.(1)求椭圆
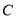 的标准方程;
的标准方程;(2)过椭圆
 的右焦点
的右焦点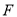 作直线
作直线 ,直线
,直线 与椭圆
与椭圆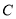 相交于
相交于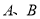 两点,当
两点,当 的面积最大时,求直线
的面积最大时,求直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

(Ⅰ)求
 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;(Ⅱ)说明函数
 的图像可由正弦曲线
的图像可由正弦曲线 经过怎样的变化得到;
经过怎样的变化得到;(Ⅲ)若
 是第二象限的角,求
是第二象限的角,求
相关试题

