【题目】已知函数![]() 的定义域为(0,+
的定义域为(0,+![]() ),若
),若![]() 在(0,+
在(0,+![]() )上为增函数,则称
)上为增函数,则称![]() 为“一阶比增函数”;若
为“一阶比增函数”;若![]() 在(0,+
在(0,+![]() )上为增函数,则称
)上为增函数,则称![]() 为”二阶比增函数”。我们把所有“一阶比增函数”组成的集合记为
为”二阶比增函数”。我们把所有“一阶比增函数”组成的集合记为![]() 1,所有“二阶比增函数”组成的集合记为
1,所有“二阶比增函数”组成的集合记为![]() 2。
2。
(1)已知函数![]() ,若
,若![]() ∈
∈![]() 1,求实数
1,求实数![]() 的取值范围,并证明你的结论;
的取值范围,并证明你的结论;
(2)已知0<a<b<c,![]() ∈
∈![]() 1且
1且![]() 的部分函数值由下表给出:
的部分函数值由下表给出:
|
|
|
|
|
|
|
| t | 4 |
求证:![]() ;
;
(3)定义集合![]() ,且存在常数k,使得任取x∈(0,+
,且存在常数k,使得任取x∈(0,+![]() ),
),![]() <k},请问:是否存在常数M,使得任意的
<k},请问:是否存在常数M,使得任意的![]() ∈
∈![]() ,任意的x∈(0,+
,任意的x∈(0,+![]() ),有
),有![]() <M成立?若存在,求出M的最小值;若不存在,说明理由。
<M成立?若存在,求出M的最小值;若不存在,说明理由。
参考答案:
【答案】(1)![]() ≤0;(2)见解析;(3)0
≤0;(2)见解析;(3)0
【解析】
(1)由![]() ∈
∈![]() ,即
,即![]() 在(0,+
在(0,+![]() )是增函数,利用单调性的定义求解即可;
)是增函数,利用单调性的定义求解即可;
(2)由f(x)∈Ω1,取0<x1<x2<x1+x2,可得![]() .由表格可知:f(a)=d,f(b)=d,f(c)=t,f(a+b+c)=4,0<a<b<c<a+b+c,利用“一阶比增函数”可得
.由表格可知:f(a)=d,f(b)=d,f(c)=t,f(a+b+c)=4,0<a<b<c<a+b+c,利用“一阶比增函数”可得![]() ,再利用不等式的性质即可得出;
,再利用不等式的性质即可得出;
(3)根据“二阶比增函数”先证明f(x)≤0对x∈(0,+∞)成立.再证明f(x)=0在(0,+∞)上无解.即可得出.
(1)解:因为![]() ∈
∈![]() ,即
,即![]() 在(0,+
在(0,+![]() )是增函数,
)是增函数,
当![]() ≤0,函数显然为增函数;
≤0,函数显然为增函数;
当![]() >0,
>0,
任取![]() ,则
,则![]()
![]()
![]() .
.
![]() ,
,![]()
当![]() ≤0,
≤0,![]() ,
,![]() , 函数为增函数
, 函数为增函数
当![]() >0,
>0,
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,即
,即![]() ,所以
,所以![]() 在
在![]() 上为减函数.
上为减函数.
当![]() 时,
时,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,即
,即![]() ,所以
,所以![]() 在
在![]() 上为增函数.
上为增函数.
所以![]() ≤0,
≤0,
(2)因为![]() ∈
∈![]() ,且0<a<b<c<a+b+c,
,且0<a<b<c<a+b+c,
所以![]() ,所以
,所以![]() ,
,
同理可证![]() ,
,![]() ,
,
三式相加得![]() ,所以
,所以![]() 。
。
因为![]() ,所以
,所以![]() ,而0<a<b,所以d<0,所以
,而0<a<b,所以d<0,所以![]() 。
。
(3)因为集合![]() ,且存在常数k,使得任取x∈(0,+
,且存在常数k,使得任取x∈(0,+![]() ),
),![]() <k},
<k},
所以![]()
![]() ∈
∈![]() ,存在常数k,使得
,存在常数k,使得![]() <k对x∈(0,+
<k对x∈(0,+![]() )成立。
)成立。
我们先证明![]() ≤0对x∈(0,+
≤0对x∈(0,+![]() )成立:假设
)成立:假设![]()
![]() ∈(0,+
∈(0,+![]() ),使得
),使得![]() >0,记
>0,记![]() >0,
>0,
因为![]() 是二阶比增函数,即
是二阶比增函数,即![]() 是增函数。所以当x>
是增函数。所以当x>![]() 时,
时,![]() >
>![]() ,所以
,所以![]()
![]() ,
,
所以一定可以找到一个![]() >
>![]() ,使得
,使得![]() >
>![]() >k,这与
>k,这与![]() <k对
<k对![]() ∈(0,+
∈(0,+![]() )成立矛盾,
)成立矛盾,
![]() ≤0对x∈(0,+
≤0对x∈(0,+![]() )成立,所以
)成立,所以![]()
![]() ∈
∈![]() ,
,![]() ≤0对x∈(0,+
≤0对x∈(0,+![]() )成立。
)成立。
下面我们证明![]() 在(0,+
在(0,+![]() )上无解:
)上无解:
假设存在![]() >0,使得
>0,使得![]() =0,则因为
=0,则因为![]() 是二阶增函数,即
是二阶增函数,即![]() 是增函数,
是增函数,
一定存在![]() >
>![]() >0,
>0,![]() >
>![]() ,这与上面证明的结果矛盾。所以
,这与上面证明的结果矛盾。所以![]() 在(0,+
在(0,+![]() )上无解。
)上无解。
综上,我们得到![]()
![]() ∈
∈![]() ,
,![]() <0对
<0对![]() ∈(0,+
∈(0,+![]() )成立,
)成立,
所以存在常数M≥0,使得![]()
![]() ∈
∈![]() ,
,![]() x∈(0,+
x∈(0,+![]() ),有
),有![]() M成立,
M成立,
又令![]() =
=![]() (
(![]() >0),则
>0),则![]() <0对x∈(0,+
<0对x∈(0,+![]() )成立,
)成立,
又有![]() 在(0,+
在(0,+![]() )上是增函数,所以
)上是增函数,所以![]() ,
,
而任取常数k<0,总可以找到一个![]() >0,使得
>0,使得![]() >
>![]() 时,有
时,有![]() >k,所以M的最小值为0。
>k,所以M的最小值为0。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
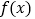 =
= +
+ ,其中a>0且a≠1。
,其中a>0且a≠1。(1)求函数
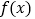 的定义域;
的定义域;(2)若函数
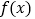 有最小值而无最大值,求
有最小值而无最大值,求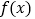 的单调增区间。
的单调增区间。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 =
=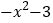 ,
, ,函数
,函数 是奇函数。
是奇函数。(1)求a,c的值;
(2)当x∈[-l,2]时,
 的最小值是1,求
的最小值是1,求 的解析式。
的解析式。 -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 =Asin
=Asin (A>0,
(A>0, >0,
>0, <
< ≤
≤ )在
)在 处取得最大值2,其图象与x轴的相邻两个交点的距离为
处取得最大值2,其图象与x轴的相邻两个交点的距离为 。
。(1)求
 的解析式;
的解析式;(2)求函数

 的值域。
的值域。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为⊙O外一点,PC交⊙O于F,C,PA切⊙O于A,B为线段PA的中点,BC交⊙O于D,线段PD的延长线与⊙O交于E,连接FE.求证:
(Ⅰ)△PBD∽△CBP;
(Ⅱ)AP∥FE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 , g(x)=ex+m , 其中e=2.718….
, g(x)=ex+m , 其中e=2.718….
(1)求f(x)在x=1处的切线方程;
(2)当m≥﹣2时,证明:f(x)<g(x). -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列说法:
①集合
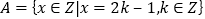 与集合
与集合 是相等集合;
是相等集合;②不存在实数
 ,使
,使 为奇函数;
为奇函数;③若
 ,且f(1)=2,则
,且f(1)=2,则 ;
;④对于函数

 在同一直角坐标系中,若
在同一直角坐标系中,若 ,则函数
,则函数 的图象关于直线
的图象关于直线 对称;
对称;⑤对于函数

 在同一直角坐标系中,函数
在同一直角坐标系中,函数 与
与 的图象关于直线
的图象关于直线 对称;其中正确说法是____________.
对称;其中正确说法是____________.
相关试题

