【题目】设函数![]() =Asin
=Asin![]() (A>0,
(A>0,![]() >0,
>0,![]() <
<![]() ≤
≤![]() )在
)在![]() 处取得最大值2,其图象与x轴的相邻两个交点的距离为
处取得最大值2,其图象与x轴的相邻两个交点的距离为![]() 。
。
(1)求![]() 的解析式;
的解析式;
(2)求函数![]()
![]() 的值域。
的值域。
参考答案:
【答案】(1)![]() =2 sin(2x+
=2 sin(2x+![]() );(2)
);(2)![]()
![]() (
(![]() ,
,![]() ]
]
【解析】
(1)先确定函数的周期,可得ω的值,利用函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,﹣π<φ<π)在x![]() 处取得最大值2,即可求得f(x)的解析式;
处取得最大值2,即可求得f(x)的解析式;
(2)由三角函数恒等变换的应用化简可得g(x)![]() ,
,![]() ,由
,由![]() ,即可求得函数g(x)的值域.
,即可求得函数g(x)的值域.
解:(1)由题意可得:f(x)max=A=2,![]() ,
,
于是![]() ,
,
故f(x)=2sin(2x+φ),
由f(x)在![]() 处取得最大值2可得:
处取得最大值2可得:![]() (k∈Z),
(k∈Z),
又﹣π<φ<π,故![]() ,
,
因此f(x)的解析式为![]() .
.
(2)由(1)可得:![]() ,
,
故![]()
![]()
![]()
![]()
![]() ,
,![]() ,
,
令t=cos2x,可知0≤t≤1且![]() ,
,
即![]() ,
,
从而![]() ,
,
因此,函数g(x)的值域为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,若对任意的m,
,若对任意的m, ,
, ,都有
,都有 .
. 若
若 ,求a的取值范围.
,求a的取值范围. 若不等式
若不等式 对任意
对任意 和
和 都恒成立,求t的取值范围.
都恒成立,求t的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
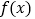 =
= +
+ ,其中a>0且a≠1。
,其中a>0且a≠1。(1)求函数
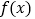 的定义域;
的定义域;(2)若函数
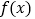 有最小值而无最大值,求
有最小值而无最大值,求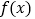 的单调增区间。
的单调增区间。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 =
=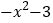 ,
, ,函数
,函数 是奇函数。
是奇函数。(1)求a,c的值;
(2)当x∈[-l,2]时,
 的最小值是1,求
的最小值是1,求 的解析式。
的解析式。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 的定义域为(0,+
的定义域为(0,+ ),若
),若 在(0,+
在(0,+ )上为增函数,则称
)上为增函数,则称 为“一阶比增函数”;若
为“一阶比增函数”;若 在(0,+
在(0,+ )上为增函数,则称
)上为增函数,则称 为”二阶比增函数”。我们把所有“一阶比增函数”组成的集合记为
为”二阶比增函数”。我们把所有“一阶比增函数”组成的集合记为 1,所有“二阶比增函数”组成的集合记为
1,所有“二阶比增函数”组成的集合记为 2。
2。(1)已知函数
 ,若
,若 ∈
∈ 1,求实数
1,求实数 的取值范围,并证明你的结论;
的取值范围,并证明你的结论;(2)已知0<a<b<c,
 ∈
∈ 1且
1且 的部分函数值由下表给出:
的部分函数值由下表给出:







t
4
求证:
 ;
;(3)定义集合
 ,且存在常数k,使得任取x∈(0,+
,且存在常数k,使得任取x∈(0,+ ),
), <k},请问:是否存在常数M,使得任意的
<k},请问:是否存在常数M,使得任意的 ∈
∈ ,任意的x∈(0,+
,任意的x∈(0,+ ),有
),有 <M成立?若存在,求出M的最小值;若不存在,说明理由。
<M成立?若存在,求出M的最小值;若不存在,说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为⊙O外一点,PC交⊙O于F,C,PA切⊙O于A,B为线段PA的中点,BC交⊙O于D,线段PD的延长线与⊙O交于E,连接FE.求证:
(Ⅰ)△PBD∽△CBP;
(Ⅱ)AP∥FE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 , g(x)=ex+m , 其中e=2.718….
, g(x)=ex+m , 其中e=2.718….
(1)求f(x)在x=1处的切线方程;
(2)当m≥﹣2时,证明:f(x)<g(x).
相关试题

