【题目】已知函数![]() =
=![]() +
+![]() ,其中a>0且a≠1。
,其中a>0且a≠1。
(1)求函数![]() 的定义域;
的定义域;
(2)若函数![]() 有最小值而无最大值,求
有最小值而无最大值,求![]() 的单调增区间。
的单调增区间。
参考答案:
【答案】(1)![]() ;(2)[﹣1,1).
;(2)[﹣1,1).
【解析】
(1)根据对数函数的成立的条件建立不等式关系即可求出函数的定义域;
(2)根据复合函数单调性的性质确定0<a<1,结合复合函数单调性的关系进行求解即可.
解:(1)要使函数有意义,则![]() ,得
,得![]() ,得﹣3<x<1,
,得﹣3<x<1,
即函数的定义域为(﹣3,1),
(2)f(x)=loga(1﹣x)+loga(x+3)=loga(1﹣x)(x+3)=loga(﹣x2﹣2x+3)
=loga(﹣(x+1)2+4),
设t=﹣(x+1)2+4,当﹣3<x<1时,0<t≤4,
若函数f(x)有最小值而无最大值,则函数ylogat为减函数,则0<a<1,
要求f(x)的单调增区间,则等价于求t=﹣(x+1)2+4,在﹣3<x<1时的减区间,
∵t=﹣(x+1)2+4的单调递减区间为[﹣1,1),
∴f(x)的单调递减区间为[﹣1,1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 的底面ABCD是正方形,
的底面ABCD是正方形, 为等边三角形,M,N分别是AB,AD的中点,且平面
为等边三角形,M,N分别是AB,AD的中点,且平面 平面ABCD.
平面ABCD.
 证明:
证明: 平面PNB;
平面PNB; 设点E是棱PA上一点,若
设点E是棱PA上一点,若 平面DEM,求
平面DEM,求 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,圆C的参数方程
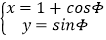 (φ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(φ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆C的极坐标方程;
(Ⅱ)直线l的极坐标方程是ρ(sinθ+ cosθ)=3
cosθ)=3 , 射线OM:θ=
, 射线OM:θ= 与圆C的交点为O,P,与直线l的交点为Q,求线段PQ的长.
与圆C的交点为O,P,与直线l的交点为Q,求线段PQ的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,若对任意的m,
,若对任意的m, ,
, ,都有
,都有 .
. 若
若 ,求a的取值范围.
,求a的取值范围. 若不等式
若不等式 对任意
对任意 和
和 都恒成立,求t的取值范围.
都恒成立,求t的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 =
=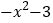 ,
, ,函数
,函数 是奇函数。
是奇函数。(1)求a,c的值;
(2)当x∈[-l,2]时,
 的最小值是1,求
的最小值是1,求 的解析式。
的解析式。 -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 =Asin
=Asin (A>0,
(A>0, >0,
>0, <
< ≤
≤ )在
)在 处取得最大值2,其图象与x轴的相邻两个交点的距离为
处取得最大值2,其图象与x轴的相邻两个交点的距离为 。
。(1)求
 的解析式;
的解析式;(2)求函数

 的值域。
的值域。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 的定义域为(0,+
的定义域为(0,+ ),若
),若 在(0,+
在(0,+ )上为增函数,则称
)上为增函数,则称 为“一阶比增函数”;若
为“一阶比增函数”;若 在(0,+
在(0,+ )上为增函数,则称
)上为增函数,则称 为”二阶比增函数”。我们把所有“一阶比增函数”组成的集合记为
为”二阶比增函数”。我们把所有“一阶比增函数”组成的集合记为 1,所有“二阶比增函数”组成的集合记为
1,所有“二阶比增函数”组成的集合记为 2。
2。(1)已知函数
 ,若
,若 ∈
∈ 1,求实数
1,求实数 的取值范围,并证明你的结论;
的取值范围,并证明你的结论;(2)已知0<a<b<c,
 ∈
∈ 1且
1且 的部分函数值由下表给出:
的部分函数值由下表给出:







t
4
求证:
 ;
;(3)定义集合
 ,且存在常数k,使得任取x∈(0,+
,且存在常数k,使得任取x∈(0,+ ),
), <k},请问:是否存在常数M,使得任意的
<k},请问:是否存在常数M,使得任意的 ∈
∈ ,任意的x∈(0,+
,任意的x∈(0,+ ),有
),有 <M成立?若存在,求出M的最小值;若不存在,说明理由。
<M成立?若存在,求出M的最小值;若不存在,说明理由。
相关试题

