【题目】如图,P为⊙O外一点,PC交⊙O于F,C,PA切⊙O于A,B为线段PA的中点,BC交⊙O于D,线段PD的延长线与⊙O交于E,连接FE.求证:
(Ⅰ)△PBD∽△CBP;
(Ⅱ)AP∥FE.
参考答案:
【答案】证明:(Ⅰ)如图,∵PA切⊙O于A,∴BA2=BDBC,
∵B为线段PA的中点,∴PB=BA,
∴PB2=BDBC,即![]() ,
,
∵∠PBD=∠CBP,∴△PBD∽△CBP.
(Ⅱ)∵△PBD∽△CBP,∴∠BPD=∠C,
∵∠C=∠E,∴∠BPD=∠E,
∴AP∥FE.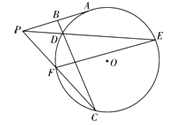
【解析】(Ⅰ)由切割线定理得BA2=BDBC,从而PB2=BDBC,由此能证明△PBD∽△CBP.
(Ⅱ)由三角形相似得∠BPD=∠C,从而∠BPD=∠E,由此能证明AP∥FE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 =
=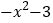 ,
, ,函数
,函数 是奇函数。
是奇函数。(1)求a,c的值;
(2)当x∈[-l,2]时,
 的最小值是1,求
的最小值是1,求 的解析式。
的解析式。 -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 =Asin
=Asin (A>0,
(A>0, >0,
>0, <
< ≤
≤ )在
)在 处取得最大值2,其图象与x轴的相邻两个交点的距离为
处取得最大值2,其图象与x轴的相邻两个交点的距离为 。
。(1)求
 的解析式;
的解析式;(2)求函数

 的值域。
的值域。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 的定义域为(0,+
的定义域为(0,+ ),若
),若 在(0,+
在(0,+ )上为增函数,则称
)上为增函数,则称 为“一阶比增函数”;若
为“一阶比增函数”;若 在(0,+
在(0,+ )上为增函数,则称
)上为增函数,则称 为”二阶比增函数”。我们把所有“一阶比增函数”组成的集合记为
为”二阶比增函数”。我们把所有“一阶比增函数”组成的集合记为 1,所有“二阶比增函数”组成的集合记为
1,所有“二阶比增函数”组成的集合记为 2。
2。(1)已知函数
 ,若
,若 ∈
∈ 1,求实数
1,求实数 的取值范围,并证明你的结论;
的取值范围,并证明你的结论;(2)已知0<a<b<c,
 ∈
∈ 1且
1且 的部分函数值由下表给出:
的部分函数值由下表给出:







t
4
求证:
 ;
;(3)定义集合
 ,且存在常数k,使得任取x∈(0,+
,且存在常数k,使得任取x∈(0,+ ),
), <k},请问:是否存在常数M,使得任意的
<k},请问:是否存在常数M,使得任意的 ∈
∈ ,任意的x∈(0,+
,任意的x∈(0,+ ),有
),有 <M成立?若存在,求出M的最小值;若不存在,说明理由。
<M成立?若存在,求出M的最小值;若不存在,说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 , g(x)=ex+m , 其中e=2.718….
, g(x)=ex+m , 其中e=2.718….
(1)求f(x)在x=1处的切线方程;
(2)当m≥﹣2时,证明:f(x)<g(x). -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列说法:
①集合
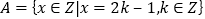 与集合
与集合 是相等集合;
是相等集合;②不存在实数
 ,使
,使 为奇函数;
为奇函数;③若
 ,且f(1)=2,则
,且f(1)=2,则 ;
;④对于函数

 在同一直角坐标系中,若
在同一直角坐标系中,若 ,则函数
,则函数 的图象关于直线
的图象关于直线 对称;
对称;⑤对于函数

 在同一直角坐标系中,函数
在同一直角坐标系中,函数 与
与 的图象关于直线
的图象关于直线 对称;其中正确说法是____________.
对称;其中正确说法是____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】在扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费的开支3 600元后,逐步偿还转让费(不计息).在甲提供的资料中:①这种消费品的进价为每件14元;②该店月销量Q(百件)与销售价格P(元)的关系如图所示;③每月需各种开支2 000元.

(1)当商品的价格为每件多少元时,月利润扣除职工最低生活费的余额最大?并求最大余额;
(2)企业乙只依靠该店,最早可望在几年后脱贫?
相关试题

