【题目】为了解喜好体育运动是否与性别有关,某报记者随机采访50个路人,将调查情况进行整理后制成下表:
年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
频数 | 5 | 10 | 8 | 10 | 5 | 5 |
喜好人数 | 4 | 6 | 6 | 3 | 3 |
(1)在调查的结果中,喜好体育运动的女性有10人,不喜好体育运动的男性有5人,请将下面的2×2列联表补充完整,并判断能否在犯错误的概率不超过0.005的前提下认为喜好体育运动与性别有关?说明你的理由;
喜好体育运动 | 不喜好体育运动 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
(2)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行追踪调查,记选中的4人中不喜好体育运动的人数为X,求随机变量X的分布列和数学期望. 下面的临界值表供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
参考答案:
【答案】
(1)解:根据频率分布表知,喜好体育运动的人数为30,则不喜好体育运动的人数为20,
填写2×2列联表如下:
喜好体育运动 | 不喜好体育运动 | 合计 | |
男生 | 20 | 5 | 25 |
女生 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
根据列联表中数据,计算
K2= ![]() =
= ![]() =3<7.879,
=3<7.879,
对照临界值知,在犯错误的概率不超过0.005的前提下,不能认为喜好体育运动与性别有关;
(2)解:从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行追踪调查,
记选中的4人中不喜好体育运动的人数为X,
依题意得X=0,1,2,3,
P(X=0)= ![]()
![]() =
= ![]() ,
,
P(X=1)= ![]()
![]() +
+ ![]()
![]() =
= ![]() ,
,
P(X=2)= ![]()
![]() +
+ ![]()
![]() =
= ![]() ,
,
P(X=3)= ![]()
![]() =
= ![]() ,
,
∴X的分布列是:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
∴X的数学期望EX=0× ![]() +1×
+1× ![]() +2×
+2× ![]() +3×
+3× ![]() =
= ![]()
【解析】(1)根据频率分布表,计算喜好体育运动和不喜好体育运动的人数,填写列联表,计算K2,对照临界值得出结论;(2)根据题意知随机变量X的可能取值,计算对应的概率值,写出分布列,计算数学期望值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a、b是方程2(lg x)2-lg x6+3=0的两个实根,求lg(ab)·(logab+logba)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=
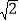 a,
a,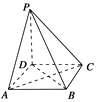
(1)求证:PD⊥平面ABCD;
(2)求证:平面PAC⊥平面PBD;
(3)求二面角P-AC-D的正切值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2015·湖南)如下图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E、F分别是BC、CC1的中点.
(1)证明:平面AEF⊥平面B1BCC1;
(2)若直线A1C与平面A1ABB1所成的角为45°,求三棱锥F-AEC的体积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】要建造一个容积为1 600立方米,深为4米的长方体无盖蓄水池,池壁的造价为每平方米200元,池底的造价为每平方米100元.
(1)把总造价y元表示为池底的一边长x米的函数;
(2)由于场地原因,蓄水池的一边长不能超过20米,问蓄水池的这个底边长为多少时总造价最低?总造价最低是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂今年拟举行促销活动,经调查测算,该厂产品的年销售量(即该厂的年产量)x(万件)与年促销费m(万元)(m≥0)满足x=3-
 .已知今年生产的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
.已知今年生产的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).(1)将今年该产品的利润y(万元)表示为年促销费m(万元)的函数;
(2)求今年该产品利润的最大值,此时促销费为多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知右焦点为F(c,0)的椭圆M:
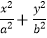 =1(a>b>0)过点
=1(a>b>0)过点 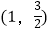 ,且椭圆M关于直线x=c对称的图形过坐标原点.
,且椭圆M关于直线x=c对称的图形过坐标原点.
(1)求椭圆M的方程;
(2)过点(4,0)且不垂直于y轴的直线与椭圆M交于P,Q两点,点Q关于x轴的对称原点为E,证明:直线PE与x轴的交点为F.
相关试题

