【题目】若a、b是方程2(lg x)2-lg x6+3=0的两个实根,求lg(ab)·(logab+logba)的值.
参考答案:
【答案】12
【解析】原方程可化为2(lg x)2-6lg x+3=0.
设t=lg x,则方程化为2t2-6t+3=0,
设t1,t2为此方程的两个实根,
则t1+t2=3,t1·t2=![]() .
.
又∵a、b是方程2(lg x)2-lg x6+3=0的两个实根,
∴可令t1=lg a,t2=lg b,
即lg a+lg b=3,lg a·lg b=![]() .
.
∴lg(ab)·(logab+logba)
=(lg a+lg b)·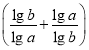
=(lg a+lg b)·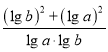
=(lg a+lg b)·
=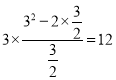 ,
,
即lg(ab)·(logab+logba)=12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】集合A是由满足以下性质的函数f(x)组成的:对于任意x≥0,f(x) ∈[-2,4]且f(x)在[0,+∞)上是增函数.
(Ⅰ)试判断
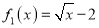 与
与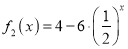 (x≥0)是否属于集合A,并说明理由;
(x≥0)是否属于集合A,并说明理由;(Ⅱ)对于(Ⅰ)中你认为属于集合A的函数f(x),证明:对于任意的x≥0,都有f(x)+f(x+2)<2f(x+1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递减,若f(log2a)+f(3
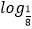 a)≥2f(﹣1),则实数a的取值范围是( )
a)≥2f(﹣1),则实数a的取值范围是( )
A.[2,4]
B.[ ,2]
,2]
C.[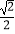 ,4]
,4]
D.[ ,2]
,2] -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱ABC﹣A1B1C1中,D是A1B1的中点.
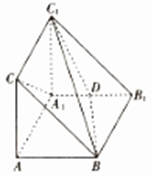
(1)求证:A1C∥平面BDC1;
(2)若AB⊥AC,且AB=AC= AA1 , 求二面角A﹣BD﹣C1的余弦值.
AA1 , 求二面角A﹣BD﹣C1的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=
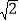 a,
a,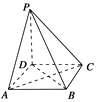
(1)求证:PD⊥平面ABCD;
(2)求证:平面PAC⊥平面PBD;
(3)求二面角P-AC-D的正切值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2015·湖南)如下图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E、F分别是BC、CC1的中点.
(1)证明:平面AEF⊥平面B1BCC1;
(2)若直线A1C与平面A1ABB1所成的角为45°,求三棱锥F-AEC的体积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解喜好体育运动是否与性别有关,某报记者随机采访50个路人,将调查情况进行整理后制成下表:
年龄(岁)
[15,25)
[25,35)
[35,45)
15[45,55)
[55,65)
[65,75)
频数
5
10
8
10
5
5
喜好人数
4
6
6
3
3
(1)在调查的结果中,喜好体育运动的女性有10人,不喜好体育运动的男性有5人,请将下面的2×2列联表补充完整,并判断能否在犯错误的概率不超过0.005的前提下认为喜好体育运动与性别有关?说明你的理由;喜好体育运动
不喜好体育运动
合计
男生
5
女生
10
合计
50
(2)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行追踪调查,记选中的4人中不喜好体育运动的人数为X,求随机变量X的分布列和数学期望. 下面的临界值表供参考:P(K2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式:K2=
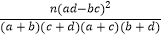 ,其中n=a+b+c+d)
,其中n=a+b+c+d)
相关试题

