【题目】如图所示,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=![]() a,
a,
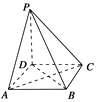
(1)求证:PD⊥平面ABCD;
(2)求证:平面PAC⊥平面PBD;
(3)求二面角P-AC-D的正切值.
参考答案:
【答案】(1)见解析(2)见解析(3)![]()
【解析】(1)证明:∵PD=a,DC=a,PC=![]() a,∴PC2=PD2+DC2,
a,∴PC2=PD2+DC2,
∴PD⊥DC.同理,PD⊥AD,又AD∩DC=D,∴PD⊥平面ABCD.
(2)证明:由(1)知PD⊥平面ABCD,∴PD⊥AC,又四边形ABCD是正
方形,∴AC⊥BD,又BD∩PD=D,∴AC⊥平面PDB.又AC平面PAC,
∴平面PAC⊥平面PBD.
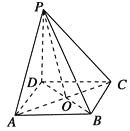
(3)设AC∩BD=O,连接PO.由PA=PC,知PO⊥AC.又DO⊥AC,故∠POD为二面角P-AC-D的平面角.易知OD=![]() .
.
在Rt△PDO中,tan∠POD= .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点.将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2.
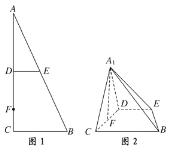
(1)求证:DE∥平面A1CB;
(2)求证:A1F⊥BE;
(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
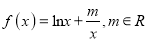 .
.(1)当
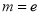 (
(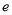 为自然对数的底数)时,求
为自然对数的底数)时,求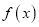 的最小值;
的最小值;(2)讨论函数
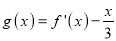 零点的个数;
零点的个数;(3)若对任意
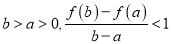 恒成立,求
恒成立,求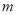 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 ,
,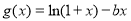 .
.(1)若函数
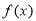 在
在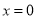 处有极值,求函数
处有极值,求函数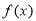 的最大值;
的最大值;(2)①是否存在实数
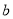 ,使得关于
,使得关于 的不等式
的不等式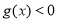 在
在 上恒成立?若存在,求出
上恒成立?若存在,求出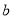 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;②证明:不等式
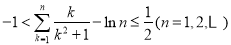 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E,F分别是AP,AD的中点.
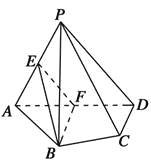
求证:(1)直线EF∥平面PCD;
(2)平面BEF⊥平面PAD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
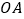 、
、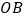 是两条公路(近似看成两条直线),
是两条公路(近似看成两条直线),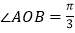 ,在
,在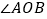 内有一纪念塔
内有一纪念塔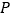 (大小忽略不计),已知
(大小忽略不计),已知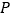 到直线
到直线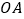 、
、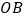 的距离分别为
的距离分别为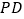 、
、 ,
,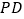 =6千米,
=6千米, =12千米.现经过纪念塔
=12千米.现经过纪念塔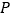 修建一条直线型小路,与两条公路
修建一条直线型小路,与两条公路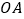 、
、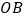 分别交于点
分别交于点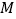 、
、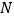 .
.(1)求纪念塔
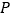 到两条公路交点
到两条公路交点 处的距离;
处的距离;(2)若纪念塔
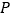 为小路
为小路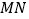 的中点,求小路
的中点,求小路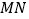 的长.
的长.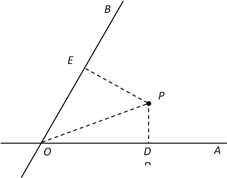
-
科目: 来源: 题型:
查看答案和解析>>【题目】为推行“微课、翻转课堂”教学法,某数学老师分别用传统教学和“微课、翻转课堂”两种不同的教学方式,在甲、乙两个平行班级进行教学实验,为了比较教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,结果如下表:
记成绩不低于70分者为“成绩优良”.

(1)由以上统计数据填写下面
 列联表,并判断“成绩优良与教学方式是否有关”?
列联表,并判断“成绩优良与教学方式是否有关”?
附:
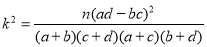
临界值表:

(2)现从上述40人中,学校按成绩是否优良采用分层抽样的方法抽取8人进行考核,在这8人中,记成绩不优良的乙班人数为
 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
相关试题

