【题目】已知函数f(x)=![]() ax3+ax2﹣3ax+1的图象经过四个象限,则实数a的取值范围为
ax3+ax2﹣3ax+1的图象经过四个象限,则实数a的取值范围为
参考答案:
【答案】(﹣∞,﹣![]() )∪(
)∪(![]() , +∞)
, +∞)
【解析】解:∵f(x)=![]() ax3+ax2﹣3ax+1,
ax3+ax2﹣3ax+1,
∴f′(x)=ax2+2ax﹣3a=a(x﹣1)(x+3),
令f′(x)=0,
解的x=1或x=﹣3,是函数的极值点,当a>0时,f(﹣3)是极大值,f(1)是极小值,f(﹣3)f(1)<0,当a<0时,f(﹣3)是极小值,f(1)是极大值,f(﹣3)f(1)<0,
所以,要使函数f(x)的图象经过四个象限,则f(﹣3)f(1)<0,
∵f(﹣3)=![]() a(﹣3)3+a(﹣3)2﹣3a(﹣3)+1=9a+1,
a(﹣3)3+a(﹣3)2﹣3a(﹣3)+1=9a+1,
f(1)=![]() a+a﹣3a+1=1﹣
a+a﹣3a+1=1﹣![]() a,
a,
∴(9a+1)(1﹣![]() a)<0,
a)<0,
即(a+![]() )(a﹣
)(a﹣![]() )>0,
)>0,
解的a<﹣![]() , 或a>
, 或a>![]()
所以答案是:(﹣∞,﹣![]() )∪(
)∪(![]() , +∞).
, +∞).
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减,以及对函数的极值与导数的理解,了解求函数
在这个区间单调递减,以及对函数的极值与导数的理解,了解求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C的圆心C在直线
 上.
上. 若圆C与y轴的负半轴相切,且该圆截x轴所得的弦长为
若圆C与y轴的负半轴相切,且该圆截x轴所得的弦长为 ,求圆C的标准方程;
,求圆C的标准方程; 已知点
已知点 ,圆C的半径为3,且圆心C在第一象限,若圆C上存在点M,使
,圆C的半径为3,且圆心C在第一象限,若圆C上存在点M,使 为坐标原点
为坐标原点 ,求圆心C的纵坐标的取值范围.
,求圆心C的纵坐标的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列推理过程不是演绎推理的是( ).
①一切奇数都不能被2整除,2019是奇数, 2019不能被2整除;
②由“正方形面积为边长的平方”得到结论:正方体的体积为棱长的立方;
③在数列
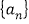 中,
中,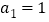 ,
,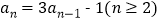 ,由此归纳出
,由此归纳出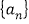 的通项公式;
的通项公式;④由“三角形内角和为
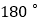 ”得到结论:直角三角形内角和为
”得到结论:直角三角形内角和为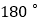 .
.A. ① ② B. ② ③ C. ③ ④ D. ②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年10月24日,世界上最长的跨海大桥一港珠澳大桥正式通车
 在一般情况下,大桥上的车流速度
在一般情况下,大桥上的车流速度 单位:千米
单位:千米 时
时 是车流密度
是车流密度 单位:辆
单位:辆 千米
千米 的函数
的函数 当桥上的车流密度达到220辆
当桥上的车流密度达到220辆 千米时,将造成堵塞,此时车流速度为0;当车流密度不超过20辆
千米时,将造成堵塞,此时车流速度为0;当车流密度不超过20辆 千米时,车流速度为100千米
千米时,车流速度为100千米 时,研究表明:当
时,研究表明:当 时,车流速度v是车流密度x的一次函数.
时,车流速度v是车流密度x的一次函数. Ⅰ
Ⅰ 当
当 时,求函数
时,求函数 的表达式;
的表达式; Ⅱ
Ⅱ 当车流密度x为多大时,车流量
当车流密度x为多大时,车流量 单位时间内通过桥上某观测点的车辆数,单位:辆
单位时间内通过桥上某观测点的车辆数,单位:辆 时
时 可以达到最大?并求出最大值.
可以达到最大?并求出最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 =(2﹣sin(2x+
=(2﹣sin(2x+ ),﹣2),
),﹣2), =(1,sin2x),f(x)=
=(1,sin2x),f(x)=
 , (x∈[0,
, (x∈[0, ])
])
(1)求函数f(x)的值域;
(2)设△ABC的内角A,B,C的对边长分别为a,b,c,若f( )=1,b=1,c=
)=1,b=1,c= , 求a的值.
, 求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数h(x)=x﹣(a+1)lnx﹣
 , 求函数h(x)的单调递减区间.
, 求函数h(x)的单调递减区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列类比推理命题(其中
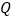 为有理数集,
为有理数集,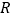 为实数集,
为实数集,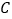 为复数集),其中类比结论正确的是( )
为复数集),其中类比结论正确的是( )A. “若
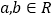 ,则
,则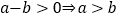 ”类比推出“若
”类比推出“若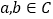 ,则
,则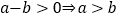 ”.
”.B.
 类比推出
类比推出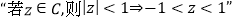
C.
 类比推出
类比推出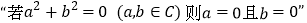
D. “若
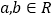 ,则
,则 ”类比推出“若
”类比推出“若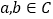 ,则
,则 ”.
”.
相关试题

