【题目】已知![]() =(2﹣sin(2x+
=(2﹣sin(2x+![]() ),﹣2),
),﹣2),![]() =(1,sin2x),f(x)=
=(1,sin2x),f(x)=![]()
![]() , (x∈[0,
, (x∈[0,![]() ])
])
(1)求函数f(x)的值域;
(2)设△ABC的内角A,B,C的对边长分别为a,b,c,若f(![]() )=1,b=1,c=
)=1,b=1,c=![]() , 求a的值.
, 求a的值.
参考答案:
【答案】解:(1)f(x)=![]()
![]() =2﹣sin(2x+
=2﹣sin(2x+![]() )﹣2sin2x=2﹣(sin2xcos
)﹣2sin2x=2﹣(sin2xcos![]() +cos2xsin
+cos2xsin![]() )﹣(1﹣cos2x)=
)﹣(1﹣cos2x)=![]() cos2x﹣
cos2x﹣![]() sin2x+1=cos(2x+
sin2x+1=cos(2x+![]() )+1.
)+1.
∵x∈[0,![]() ],∴2x+
],∴2x+![]() ∈[
∈[![]() ,
,![]() ],∴﹣1≤cos(2x+
],∴﹣1≤cos(2x+![]() )≤
)≤![]() ,从而有0≤f(x)≤
,从而有0≤f(x)≤![]() ,
,
所以函数f(x)的值域为[0,![]() ].
].
(2)由f(![]() )=1,得cos(B+
)=1,得cos(B+![]() )=0,又因为0<B<π,所以
)=0,又因为0<B<π,所以![]() <B+
<B+![]()
![]()
![]() ,
,
从而B+![]() =
=![]() ,即B=
,即B=![]() .
.
因为b=1,c=![]() ,所以由正弦定理
,所以由正弦定理![]() 得sinC=
得sinC=![]() =
=![]() ,
,
故C=![]() 或
或![]() ,
,
当C=![]() 时,A=
时,A=![]() ,从而a=
,从而a=![]() =2,
=2,
当C=![]() 时,A=
时,A=![]() ,又B=
,又B=![]() ,从而a=b=1
,从而a=b=1
综上a的值为1或2
【解析】(1)利用平面向量数量积的运算及三角函数恒等变换的应用化简可得解析式f(x)=cos(2x+![]() )+1,由余弦函数的有界性即可求值域.
)+1,由余弦函数的有界性即可求值域.
(2)由f(![]() )=1,得cos(B+
)=1,得cos(B+![]() )=0,又结合范围0<B<π,即可解得B的值,由正弦定理可求sinC,解得C,解得A,即可解得a的值.
)=0,又结合范围0<B<π,即可解得B的值,由正弦定理可求sinC,解得C,解得A,即可解得a的值.
【考点精析】掌握两角和与差的正弦公式和正弦定理的定义是解答本题的根本,需要知道两角和与差的正弦公式:![]() ;正弦定理:
;正弦定理:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列推理过程不是演绎推理的是( ).
①一切奇数都不能被2整除,2019是奇数, 2019不能被2整除;
②由“正方形面积为边长的平方”得到结论:正方体的体积为棱长的立方;
③在数列
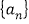 中,
中,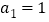 ,
,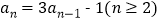 ,由此归纳出
,由此归纳出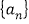 的通项公式;
的通项公式;④由“三角形内角和为
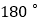 ”得到结论:直角三角形内角和为
”得到结论:直角三角形内角和为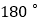 .
.A. ① ② B. ② ③ C. ③ ④ D. ②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年10月24日,世界上最长的跨海大桥一港珠澳大桥正式通车
 在一般情况下,大桥上的车流速度
在一般情况下,大桥上的车流速度 单位:千米
单位:千米 时
时 是车流密度
是车流密度 单位:辆
单位:辆 千米
千米 的函数
的函数 当桥上的车流密度达到220辆
当桥上的车流密度达到220辆 千米时,将造成堵塞,此时车流速度为0;当车流密度不超过20辆
千米时,将造成堵塞,此时车流速度为0;当车流密度不超过20辆 千米时,车流速度为100千米
千米时,车流速度为100千米 时,研究表明:当
时,研究表明:当 时,车流速度v是车流密度x的一次函数.
时,车流速度v是车流密度x的一次函数. Ⅰ
Ⅰ 当
当 时,求函数
时,求函数 的表达式;
的表达式; Ⅱ
Ⅱ 当车流密度x为多大时,车流量
当车流密度x为多大时,车流量 单位时间内通过桥上某观测点的车辆数,单位:辆
单位时间内通过桥上某观测点的车辆数,单位:辆 时
时 可以达到最大?并求出最大值.
可以达到最大?并求出最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 ax3+ax2﹣3ax+1的图象经过四个象限,则实数a的取值范围为
ax3+ax2﹣3ax+1的图象经过四个象限,则实数a的取值范围为 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数h(x)=x﹣(a+1)lnx﹣
 , 求函数h(x)的单调递减区间.
, 求函数h(x)的单调递减区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列类比推理命题(其中
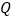 为有理数集,
为有理数集,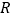 为实数集,
为实数集,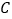 为复数集),其中类比结论正确的是( )
为复数集),其中类比结论正确的是( )A. “若
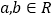 ,则
,则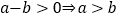 ”类比推出“若
”类比推出“若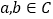 ,则
,则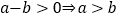 ”.
”.B.
 类比推出
类比推出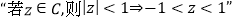
C.
 类比推出
类比推出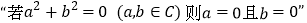
D. “若
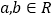 ,则
,则 ”类比推出“若
”类比推出“若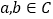 ,则
,则 ”.
”. -
科目: 来源: 题型:
查看答案和解析>>【题目】将5名报名参加运动会的同学分别安排到跳绳、接力,投篮三项比赛中(假设这些比赛都不设人数上限),每人只参加一项,则共有
 种不同的方案;若每项比赛至少要安排一人时,则共有
种不同的方案;若每项比赛至少要安排一人时,则共有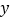 种不同的方案,其中
种不同的方案,其中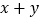 的值为( )
的值为( )A. 543 B. 425 C. 393 D. 275
相关试题

