搜索
【题目】某大学的
名同学准备拼车去旅游，其中大一、大二、大三、大四每个年级各两名，分乘甲、乙两辆汽车，每车限坐
名同学（乘同一辆车的
名同学不考虑位置），其中大一的孪生姐妹需乘同一辆车，则乘坐甲车的
名同学中恰有
名同学是来自于同一年级的乘坐方式共有（ ）．
A. 
种 B. 
种 C. 
种 D. 
种
参考答案：
【答案】B
【解析】试题分析：由题意，第一类，一年级的孪生姐妹在甲车上，甲车上剩下两个要来自不同的年级，从三个年级中选两个为
，然后分别从选择的年级中再选择一个学生为
，故有3×4=12种．
第二类，一年级的孪生姐妹不在甲车上，则从剩下的3个年级中选择一个年级的两名同学在甲车上，为
，然后再从剩下的两个年级中分别选择一人为
，这时共有3×4=12种
根据分类计数原理得，共有12+12=24种不同的乘车方式
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xoy中，已知直线l：x+y+a=0与点A（0，2），若直线l上存在点M满足|MA|2+|MO|2=10（O为坐标原点），则实数a的取值范围是（ ）
A.（﹣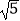
﹣1， ﹣1）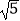
B.[﹣ ﹣1， ﹣1]
C.（﹣2
﹣1，2 ﹣1）
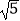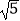D.[﹣2 ﹣1，2 ﹣1] -
科目： 来源： 题型：
查看答案和解析>>【题目】已知关于x的方程为2kx2﹣2x﹣5k﹣2＝0的两个实数根一个小于1，另一个大于1，则实数k的取值范围是（ ）
A.
B. 
C. 
D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】有下列四个命题：
①已知-1＜a＜b＜0，则0.3a＞a2＞ab；
②若正实数a、b满足a+b=1，则ab有最大值
；③若正实数a、b满足a+b=1，则
有最大值
；④x，y∈（0，+∞），x3+y3＞x2y+xy2．
其中真命题的个数是（ ）
A. 1 B. 2 C. 3 D. 4
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=x2（ex+e﹣x）﹣（2x+1）2（e2x+1+e﹣2x﹣1），则满足f（x）＞0的实数x的取值范围为（ ）
A.（﹣1，﹣
）
B.（﹣∞，﹣1）
C.（﹣ ，+∞）
D.（﹣∞，﹣1）∪（﹣ ，+∞） -
科目： 来源： 题型：
查看答案和解析>>【题目】（m+x）（1+x）3的展开式中x的奇数次幂项的系数之和为16，则
xmdx= ． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知中心在原点的椭圆与双曲线有公共焦点，且左、右焦点分别为F1、F2 ， 这两条曲线在第一象限的交点为P，△PF1F2 是以PF1为底边的等腰三角形．若|PF1|=10，椭圆与双曲线的离心率分别为e1、e2 ， 则e1e2 的取值范围为 ．
相关试题
