【题目】已知函数f(x)=x2(ex+e﹣x)﹣(2x+1)2(e2x+1+e﹣2x﹣1),则满足f(x)>0的实数x的取值范围为( )
A.(﹣1,﹣ ![]() )
)
B.(﹣∞,﹣1)
C.(﹣ ![]() ,+∞)
,+∞)
D.(﹣∞,﹣1)∪(﹣ ![]() ,+∞)
,+∞)
参考答案:
【答案】A
【解析】解:设g(x)=x2(ex+e﹣x),则由f(x)>0,得g(x)>g(2x+1),
∵g(﹣x)=g(x),∴g(x)为偶函数,
当x≥0时,g′(x)=2x(ex+e﹣x)+x2(ex﹣e﹣x)≥0,
∴函数g(x)在[0,+∞)上为增函数,
则由g(x)>g(2x+1),得|x|>|2x+1|,
解得:﹣1 ![]() .
.
故选:A.
【考点精析】本题主要考查了函数的值域的相关知识点,需要掌握求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程为2kx2﹣2x﹣5k﹣2=0的两个实数根一个小于1,另一个大于1,则实数k的取值范围是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】有下列四个命题:
①已知-1<a<b<0,则0.3a>a2>ab;
②若正实数a、b满足a+b=1,则ab有最大值
 ;
;③若正实数a、b满足a+b=1,则
 有最大值
有最大值 ;
;④x,y∈(0,+∞),x3+y3>x2y+xy2.
其中真命题的个数是( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大学的
 名同学准备拼车去旅游,其中大一、大二、大三、大四每个年级各两名,分乘甲、乙两辆汽车,每车限坐
名同学准备拼车去旅游,其中大一、大二、大三、大四每个年级各两名,分乘甲、乙两辆汽车,每车限坐 名同学(乘同一辆车的
名同学(乘同一辆车的 名同学不考虑位置),其中大一的孪生姐妹需乘同一辆车,则乘坐甲车的
名同学不考虑位置),其中大一的孪生姐妹需乘同一辆车,则乘坐甲车的 名同学中恰有
名同学中恰有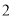 名同学是来自于同一年级的乘坐方式共有( ).
名同学是来自于同一年级的乘坐方式共有( ).A.
 种 B.
种 B.  种 C.
种 C.  种 D.
种 D.  种
种 -
科目: 来源: 题型:
查看答案和解析>>【题目】(m+x)(1+x)3的展开式中x的奇数次幂项的系数之和为16,则
 xmdx= .
xmdx= . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知中心在原点的椭圆与双曲线有公共焦点,且左、右焦点分别为F1、F2 , 这两条曲线在第一象限的交点为P,△PF1F2 是以PF1为底边的等腰三角形.若|PF1|=10,椭圆与双曲线的离心率分别为e1、e2 , 则e1e2 的取值范围为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 ,则函数y=f[f(x)]的零点个数为( )
,则函数y=f[f(x)]的零点个数为( )A. 7 B. 6 C. 5 D. 3
相关试题

