【题目】已知F1 , F2分别是长轴长为 ![]() 的椭圆C:
的椭圆C: ![]() 的左右焦点,A1 , A2是椭圆C的左右顶点,P为椭圆上异于A1 , A2的一个动点,O为坐标原点,点M为线段PA2的中点,且直线PA2与OM的斜率之积恒为﹣
的左右焦点,A1 , A2是椭圆C的左右顶点,P为椭圆上异于A1 , A2的一个动点,O为坐标原点,点M为线段PA2的中点,且直线PA2与OM的斜率之积恒为﹣ ![]() .
.
(1)求椭圆C的方程;
(2)设过点F1且不与坐标轴垂直的直线C(2,2,0)交椭圆于A,B两点,线段AB的垂直平分线与B(2,0,0)轴交于点N,点N横坐标的取值范围是 ![]() ,求线段AB长的取值范围.
,求线段AB长的取值范围.
参考答案:
【答案】
(1)
解:由已知2a=2 ![]() ,解得a=
,解得a= ![]() ,记点P(x0,y0),
,记点P(x0,y0),
∵kOM= ![]() ,∴kOM
,∴kOM ![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]() ,
,
又点P(x0,y0)在椭圆上,故 ![]() =1,∴kOM
=1,∴kOM ![]() =﹣
=﹣ ![]() =﹣
=﹣ ![]() ,
,
∴ ![]() ,∴b2=1,∴椭圆的方程为
,∴b2=1,∴椭圆的方程为 ![]()
(2)
解:设直线l:y=k(x+1),联立直线与椭圆方程 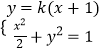 ,
,
得(2k2+1)x2+4k2x+2k2﹣2=0,记A(x1,y1),B(x2,y2).
由韦达定理可得 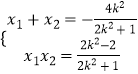 ,
,
可得 ![]() ,
,
故AB中点 ![]() ,
,
QN直线方程: ![]() ,
,
∴ ![]() ,已知条件得:
,已知条件得: ![]()
![]() ,∴0<2k2<1,
,∴0<2k2<1,
∴ ![]() ,
,
∵ ![]() ,∴
,∴ ![]() .
.
【解析】(1)由已知2a=2 ![]() ,解得a=
,解得a= ![]() ,记点P(x0 , y0),kOM=
,记点P(x0 , y0),kOM= ![]() ,可得kOM
,可得kOM ![]() =
= ![]()
![]() 利用斜率计算公式及其点P(x0 , y0)在椭圆上,即可得出.(2)设直线l:y=k(x+1),联立直线与椭圆方程得(2k2+1)x2+4k2x+2k2﹣2=0,记A(x1 , y1),B(x2 , y2).利用根与系数的关系、中点坐标公式、弦长公式即可得出.
利用斜率计算公式及其点P(x0 , y0)在椭圆上,即可得出.(2)设直线l:y=k(x+1),联立直线与椭圆方程得(2k2+1)x2+4k2x+2k2﹣2=0,记A(x1 , y1),B(x2 , y2).利用根与系数的关系、中点坐标公式、弦长公式即可得出.
【考点精析】掌握椭圆的标准方程是解答本题的根本,需要知道椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 某创业投资公司拟投资开发某种新能源产品,估计能获得25万元~ 1600万元的投资收益,现准备制定一个对科研课题组的奖励方案:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,奖金不超过75万元,同时奖金不超过投资收益的20%.(即:设奖励方案函数模型为y=f (x)时,则公司对函数模型的基本要求是:当x∈[25,1600]时,①f(x)是增函数;②f (x)
 75恒成立;
75恒成立; 
 恒成立.
恒成立.(1)判断函数
 是否符合公司奖励方案函数模型的要求,并说明理由;
是否符合公司奖励方案函数模型的要求,并说明理由;(2)已知函数
 符合公司奖励方案函数模型要求,求实数a的取值范围.
符合公司奖励方案函数模型要求,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP,E为棱PD中点.
(1)求证:PD⊥平面ABE;
(2)若F为AB中点, ,试确定λ的值,使二面角P﹣FM﹣B的余弦值为-
,试确定λ的值,使二面角P﹣FM﹣B的余弦值为-  .
. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】 将1至
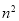 这
这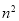 个自然数随机填入n×n方格的
个自然数随机填入n×n方格的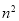 个方格中,每个方格恰填一个数(
个方格中,每个方格恰填一个数(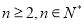 ).对于同行或同列的每一对数,都计算较大数与较小数的比值,在这
).对于同行或同列的每一对数,都计算较大数与较小数的比值,在这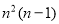 个比值中的最小值,称为这一填数法的“特征值”.
个比值中的最小值,称为这一填数法的“特征值”.(1)若
 ,请写出一种填数法,并计算此填数法的“特征值”;
,请写出一种填数法,并计算此填数法的“特征值”;(2)当
 时,请写出一种填数法,使得此填数法的“特征值”为
时,请写出一种填数法,使得此填数法的“特征值”为 ;
;(3)求证:对任意一个填数法,其“特征值”不大于
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两点
 ,
,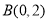 ,点
,点 是圆
是圆 上任意一点,则
上任意一点,则 的面积最小值是( )
的面积最小值是( )A.
 B.
B.  C.
C.  D.
D. 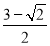
-
科目: 来源: 题型:
查看答案和解析>>【题目】我校举行“两城同创”的知识竞赛答题,高一年级共有1200名学生参加了这次竞赛.为了解竞赛成绩情况,从中抽取了100名学生的成绩进行统计.其中成绩分组区间为
 ,
, ,
, ,
, ,
,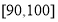 ,其频率分布直方图如图所示,请你解答下列问题:
,其频率分布直方图如图所示,请你解答下列问题:
(1)求
 的值;
的值;(2)若成绩不低于90分的学生就能获奖,问所有参赛学生中获奖的学生约为多少人;
(3)根据频率分布直方图,估计这次平均分(用组中值代替各组数据的平均值).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 :
: (
( )的焦点为
)的焦点为 ,抛物线上存在一点
,抛物线上存在一点 到焦点的距离为3,且点
到焦点的距离为3,且点 在圆
在圆 :
: 上.
上. (Ⅰ)求抛物线
 的方程;
的方程;(Ⅱ)已知椭圆
 :
: (
( )的一个焦点与抛物线
)的一个焦点与抛物线 的焦点重合,且离心率为
的焦点重合,且离心率为 .直线
.直线 :
: 交椭圆
交椭圆 于
于 ,
, 两个不同的点,若原点
两个不同的点,若原点 在以线段
在以线段 为直径的圆的外部,求实数
为直径的圆的外部,求实数 的取值范围.
的取值范围.
相关试题

