【题目】已知抛物线![]() :
:![]() (
(![]() )的焦点为
)的焦点为![]() ,抛物线上存在一点
,抛物线上存在一点![]() 到焦点的距离为3,且点
到焦点的距离为3,且点![]() 在圆
在圆![]() :
:![]() 上.
上.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)已知椭圆![]() :
:![]() (
(![]() )的一个焦点与抛物线
)的一个焦点与抛物线![]() 的焦点重合,且离心率为
的焦点重合,且离心率为![]() .直线
.直线![]() :
:![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两个不同的点,若原点
两个不同的点,若原点![]() 在以线段
在以线段![]() 为直径的圆的外部,求实数
为直径的圆的外部,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ) ![]() ( Ⅱ) 实数
( Ⅱ) 实数![]() 的取值范围是
的取值范围是![]()
![]()
【解析】分析:(1)设点![]() 的坐标为
的坐标为![]() ,列出关于
,列出关于![]() 的方程组,即可求解抛物线方程;
的方程组,即可求解抛物线方程;
(2)利用已知条件推出m、n的关系,设![]() ,
,![]() ,联立直线与椭圆方程,利用韦达定理以及判别式大于0,求出k的范围,通过原点O在以线段AB为直径
,联立直线与椭圆方程,利用韦达定理以及判别式大于0,求出k的范围,通过原点O在以线段AB为直径
的圆的外部,推出![]() ,然后求解k的范围即可.
,然后求解k的范围即可.
详解:(Ⅰ)设点![]() 的坐标为
的坐标为![]() .
.
由题可知 ,解得
,解得![]() ,
,![]() ,
,![]() ,
,![]() 抛物线
抛物线![]() 的方程为
的方程为![]() ;
;
(Ⅱ)由(Ⅰ)得,抛物线![]() 的焦点
的焦点![]() ,
,
![]() 椭圆
椭圆![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点重合,
的焦点重合,![]() 椭圆
椭圆![]() 的半焦距
的半焦距![]() ,
,
即![]() ,又椭圆
,又椭圆![]() 的离心率为
的离心率为![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,
![]() 椭圆
椭圆![]() 的方程为
的方程为![]() ,
,
设![]() ,
,![]() ,由
,由 得
得![]() ,
,
由韦达定理,得![]() ,
,![]() ,
,
由![]() ,得
,得![]() ,解得
,解得![]() 或
或![]() ,①
,①
![]() 原点
原点![]() 在以线段
在以线段![]() 的圆的外部,则
的圆的外部,则![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() ,
,
即![]() ,②
,②
由①,②得,实数![]() 的范围是
的范围是![]() 或
或![]() ,
,
即实数![]() 的取值范围是
的取值范围是![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知F1 , F2分别是长轴长为
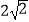 的椭圆C:
的椭圆C: 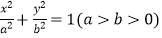 的左右焦点,A1 , A2是椭圆C的左右顶点,P为椭圆上异于A1 , A2的一个动点,O为坐标原点,点M为线段PA2的中点,且直线PA2与OM的斜率之积恒为﹣
的左右焦点,A1 , A2是椭圆C的左右顶点,P为椭圆上异于A1 , A2的一个动点,O为坐标原点,点M为线段PA2的中点,且直线PA2与OM的斜率之积恒为﹣  .
.
(1)求椭圆C的方程;
(2)设过点F1且不与坐标轴垂直的直线C(2,2,0)交椭圆于A,B两点,线段AB的垂直平分线与B(2,0,0)轴交于点N,点N横坐标的取值范围是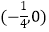 ,求线段AB长的取值范围.
,求线段AB长的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两点
 ,
,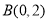 ,点
,点 是圆
是圆 上任意一点,则
上任意一点,则 的面积最小值是( )
的面积最小值是( )A.
 B.
B.  C.
C.  D.
D. 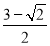
-
科目: 来源: 题型:
查看答案和解析>>【题目】我校举行“两城同创”的知识竞赛答题,高一年级共有1200名学生参加了这次竞赛.为了解竞赛成绩情况,从中抽取了100名学生的成绩进行统计.其中成绩分组区间为
 ,
, ,
, ,
, ,
,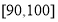 ,其频率分布直方图如图所示,请你解答下列问题:
,其频率分布直方图如图所示,请你解答下列问题:
(1)求
 的值;
的值;(2)若成绩不低于90分的学生就能获奖,问所有参赛学生中获奖的学生约为多少人;
(3)根据频率分布直方图,估计这次平均分(用组中值代替各组数据的平均值).
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年时红军长征胜利80周年,某市电视台举办纪念红军长征胜利80周年知识问答,宣传长征精神.首先在甲、乙、丙、丁四个不同的公园进行支持签名活动,其次在各公园签名的人中按分层抽样的方式抽取10名幸运之星,每人获得一个纪念品,其数据表格如下:

(Ⅰ)求此活动中各公园幸运之星的人数;
(Ⅱ)从乙和丙公园的幸运之星中任选两人接受电视台记者的采访,求这两人均来自乙公园的概率;
(Ⅲ)电视台记者对乙公园的签名人进行了是否有兴趣研究“红军长征”历史的问卷调查,统计结果如下(单位:人):

据此判断能否在犯错误的概率不超过0.01的前提下认为有兴趣研究“红军长征”历史与性别有关.
附临界值表及公式:
 ,其中
,其中
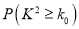
0.100
0.050
0.010
0.001

2.706
3.841
6.635
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件。已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元,现该公司至少要生产A类产品50件,B类产品140件,所需租赁费最少为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面直角坐标系内三点
 .
.(1) 求过
 三点的圆的方程,并指出圆心坐标与圆的半径;
三点的圆的方程,并指出圆心坐标与圆的半径;(2)求过点
 与条件 (1) 的圆相切的直线方程.
与条件 (1) 的圆相切的直线方程.
相关试题

