【题目】已知集合P={x|a+1≤x≤2a+1},Q={x|x2-3x≤10}.
(1)若a=3,求(RP)∩Q;
(2)若P∪Q=Q,求实数a的取值范围.
参考答案:
【答案】(1) {x|-2≤x<4};(2) (-∞,2]
【解析】
(1)解一元二次不等式得集合Q,再根据补集与交集定义求结果,(2)先根据条件得集合之间包含关系,再根据Q是否为空集分类讨论,最后求并集.
(1)因为a=3,所以P={x|4≤x≤7},
RP={x|x<4或x>7}.
又Q={x|x2-3x-10≤0}={x|-2≤x≤5},所以(RP)∩Q={x|x<4或x>7}∩{x|-2≤x≤5}={x|-2≤x<4}.
(2)当P≠时,由P∪Q=Q得PQ,
所以 解得0≤a≤2;
解得0≤a≤2;
当P=,即2a+1<a+1时,有PQ,得a<0.
综上,实数a的取值范围是(-∞,2].
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于数集
 ,其中
,其中 ,
,  ,定义向量集
,定义向量集 .若对于任意
.若对于任意 ,使得
,使得 ,则称
,则称 具有性质
具有性质 .例如
.例如 具有性质
具有性质 .
.(
 )若
)若 ,且
,且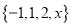 具有性质
具有性质 ,求
,求 的值.
的值.(
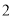 )若
)若 具有性质
具有性质 ,求证:
,求证:  ,且当
,且当 时,
时,  .
.(
 )若
)若 具有性质
具有性质 ,且
,且 ,
,  (
( 为常数),求有穷数列
为常数),求有穷数列 ,
,  ,
,  ,
,  的通项公式.
的通项公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,平面多边形
 中,AE=ED,AB=BD,且
中,AE=ED,AB=BD,且 ,现沿直线
,现沿直线 ,将
,将 折起,得到四棱锥
折起,得到四棱锥 .
.
(1)求证:
 ;
;(2)若
 ,求PD与平面
,求PD与平面 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】从甲、乙两品种的棉花中各抽测了25根棉花的纤维长度(单位:mm),得到如图5的茎叶图,整数位为茎,小数位为叶,如27.1mm的茎为27,叶为1.

(1)试比较甲、乙两种棉花的纤维长度的平均值的大小及方差的大小;(只需写出估计的结论,不需说明理由)
(2)将棉花按纤维长度的长短分成七个等级,分级标准如表:

试分别估计甲、乙两种棉花纤维长度等级为二级的概率;
(3)为进一步检验甲种棉花的其它质量指标,现从甲种棉花中随机抽取4根,记
 为抽取的棉花纤维长度为二级的根数,求
为抽取的棉花纤维长度为二级的根数,求 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,
, 是双曲线C:
是双曲线C: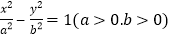 的左,右焦点,O是坐标原点
的左,右焦点,O是坐标原点 过
过 作C的一条渐近线的垂线,垂足为P,若
作C的一条渐近线的垂线,垂足为P,若 ,则C的离心率为
,则C的离心率为

A.
 B. 2 C.
B. 2 C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x∈R|x2-ax+b=0},B={x∈R|x2+cx+15=0},A∩B={3},A∪B={3,5}.
(1)求实数a,b,c的值;
(2)设集合P={x∈R|ax2+bx+c≤7},求集合P∩Z.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若
 时,对任意的
时,对任意的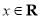 都成立,求实数
都成立,求实数 的取值范围;
的取值范围;(2)求关于
 的不等式
的不等式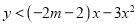 的解集.
的解集.
相关试题

