搜索
【题目】已知函数f（x）=|2x﹣1|，当a＜b＜c时，f（a）＞f（c）＞f（b），那么正确的结论是（ ）
A.2a＞2b
B.2a＞2c
C.2﹣a＜2c
D.2a+2c＜2
参考答案：
【答案】D
【解析】解：∵函数f（x）=|2x﹣1|，
∴f（x）= 
．
画出函数图象如下图所示：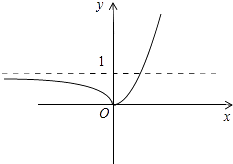
可知：函数f（x）在区间（﹣∞，0）上单调递减，在区间（0，+∞）上单调递增．
当0≤a＜b＜c时，f（x）在区间（0，+∞）上单调递增，不满足f（a）＞f（b）＞f（c），因此必有a＜0．
当a＜0＜c时，1﹣2a＞2c﹣1，化为2a+2c＜2；
当a＜b＜c≤0时，f（x）在区间（﹣∞，0]上单调递减．
∴1＞1﹣2a＞1﹣2c≥0，
∴2c≤1，2a＜1，
∴2a+2c＜2．
综上可知：D一定正确．
故选：D．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知集合A={x||x+1|＜1}，B={x|y=
，y∈R}，则A∩RB=（ ）
A.（﹣2，1）
B.（﹣2，﹣1]
C.（﹣1，0）
D.[﹣1，0） -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=
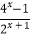，则下列关于函数f（x）的说法正确的是（ ）
A.为奇函数且在R上为增函数
B.为偶函数且在R上为增函数
C.为奇函数且在R上为减函数
D.为偶函数且在R上为减函数 -
科目： 来源： 题型：
查看答案和解析>>【题目】
已知函数f(x)＝2x3－3(a+1)x2＋6ax，a∈R．
（Ⅰ）曲线y＝f(x)在x＝0处的切线的斜率为3，求a的值；
（Ⅱ）若对于任意x∈(0，+∞)，f(x)＋f(－x)≥12lnx恒成立，求a的取值范围；
（Ⅲ）若a＞1，设函数f(x)在区间[1，2]上的最大值、最小值分别为M(a)、m(a)，
记h(a)＝M(a)－m(a)，求h(a)的最小值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在直三棱柱ABC－A1B1C1中，AB＝AC，E是BC的中点，求证：
（Ⅰ）平面AB1E⊥平面B1BCC1；
（Ⅱ）A1C//平面AB1E．
-
科目： 来源： 题型：
查看答案和解析>>【题目】试讨论函数f（x）=
在区间[0，1]上的单调性． -
科目： 来源： 题型：
查看答案和解析>>【题目】下列命题错误的是（ ）
A.命题“若x2﹣3x+2=0，则x=1”的逆否命题为“若x≠1，则x2﹣3x+2≠0”
B.若p∧q为假命题，则p，q均为假命题
C.对命题P：存在x∈R，使得x2+x+1＜0，则￢p为：任意x∈R，均有x2+x+1≥0
D.“x＞2”是“x2﹣3x+2＞0”的充分不必要条件
相关试题
