【题目】试讨论函数f(x)= ![]() 在区间[0,1]上的单调性.
在区间[0,1]上的单调性.
参考答案:
【答案】解:f(x)= ![]() 在区间[0,1]上是减函数,理由如下:
在区间[0,1]上是减函数,理由如下:
证法一:设x1、x2∈﹣1,1]且x1<x2 , 即﹣1≤x1<x2≤1.
f(x1)﹣f(x2)= ![]() ﹣
﹣ ![]() =
=  =﹣
=﹣  ,
,
∵x2﹣x1>0, ![]() >0,
>0,
∴当x1>0,x2>0时,x1+x2>0,
那么f(x1)>f(x2).
故f(x)= ![]() 在区间[0,1]上是减函数;
在区间[0,1]上是减函数;
证法二:∵函数f(x)= ![]() ,令y=
,令y= ![]() ,u=1﹣x2 ,
,u=1﹣x2 ,
则y′= ![]() ,u′=﹣2x.
,u′=﹣2x.
∴f′(x)= ![]() ,
,
当x∈[0,1)时,f′(x)≤0恒成立,f(x)>0恒成立
当x=1时,f(x)=0
故f(x)= ![]() 在区间[0,1]上是减函数
在区间[0,1]上是减函数
【解析】f(x)= ![]() 在区间[0,1]上是减函数,理由如下:
在区间[0,1]上是减函数,理由如下:
证法一:设x1、x2∈﹣1,1]且x1<x2 , 作差判断出f(x1)>f(x2)可得:f(x)= ![]() 在区间[0,1]上是减函数;
在区间[0,1]上是减函数;
证法二:求导,根据当x∈[0,1)时,f′(x)≤0恒成立,f(x)>0恒成立,当x=1时,f(x)=0可得:f(x)= ![]() 在区间[0,1]上是减函数;
在区间[0,1]上是减函数;
【考点精析】掌握函数单调性的判断方法和利用导数研究函数的单调性是解答本题的根本,需要知道单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
已知函数f(x)=2x3-3(a+1)x2+6ax,a∈R.
(Ⅰ)曲线y=f(x)在x=0处的切线的斜率为3,求a的值;
(Ⅱ)若对于任意x∈(0,+∞),f(x)+f(-x)≥12lnx恒成立,求a的取值范围;
(Ⅲ)若a>1,设函数f(x)在区间[1,2]上的最大值、最小值分别为M(a)、m(a),
记h(a)=M(a)-m(a),求h(a)的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|2x﹣1|,当a<b<c时,f(a)>f(c)>f(b),那么正确的结论是( )
A.2a>2b
B.2a>2c
C.2﹣a<2c
D.2a+2c<2 -
科目: 来源: 题型:
查看答案和解析>>【题目】在直三棱柱ABC-A1B1C1中,AB=AC,E是BC的中点,求证:
(Ⅰ)平面AB1E⊥平面B1BCC1;
(Ⅱ)A1C//平面AB1E.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题错误的是( )
A.命题“若x2﹣3x+2=0,则x=1”的逆否命题为“若x≠1,则x2﹣3x+2≠0”
B.若p∧q为假命题,则p,q均为假命题
C.对命题P:存在x∈R,使得x2+x+1<0,则¬p为:任意x∈R,均有x2+x+1≥0
D.“x>2”是“x2﹣3x+2>0”的充分不必要条件 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
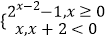 g(x)=
g(x)= 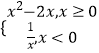 ,则函数f[g(x)]的所有零点之和是( )
,则函数f[g(x)]的所有零点之和是( )
A.
B.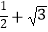
C.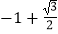
D.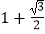
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,多面体
 中,四边形
中,四边形 是菱形,
是菱形,  ,
,  相交于
相交于 ,
,  ,点
,点 在平面
在平面 上的射影恰好是线段
上的射影恰好是线段 的中点.
的中点.
(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)若直线
 与平面
与平面 所成的角为
所成的角为 ,求平面
,求平面 与平面
与平面 所成角(锐角)的余弦值.
所成角(锐角)的余弦值.
相关试题

