【题目】已知幂函数![]() 在
在![]() 上单调递增,又函数
上单调递增,又函数![]() .
.
(1)求实数![]() 的值,并说明函数
的值,并说明函数![]() 的单调性;
的单调性;
(2)若不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)见解析;(2)![]()
【解析】
(1)由f(x)是幂函数,得到m2﹣m﹣1=1,再由f(x)在(0,+∞)上单调递增,得到﹣2m﹣1>0,从而求出m=﹣1,进而g(x)![]() ,由此能求出函数g(x)在R上单调递增;
,由此能求出函数g(x)在R上单调递增;
(2)由g(﹣x)=2﹣x![]() (
(![]() )=﹣g(x),得到g(x)是奇函数,从而不等式g(1﹣3t)+g(1+t)≥0可变为g(1﹣3t)≥﹣g(1+t)=g(﹣1﹣t),由此能求出实数t的取值范围.
)=﹣g(x),得到g(x)是奇函数,从而不等式g(1﹣3t)+g(1+t)≥0可变为g(1﹣3t)≥﹣g(1+t)=g(﹣1﹣t),由此能求出实数t的取值范围.
(1)因为![]() 是幂函数,所以
是幂函数,所以![]() ,解得
,解得![]() 或
或![]() ,
,
又因为![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,即
,即![]() ,
,
即![]() ,则
,则![]() ,
,
因为![]() 与
与![]() 均在
均在![]() 上单调递增,
上单调递增,
所以函数![]() 在
在![]() 上单调递增.
上单调递增.
(2)因为![]() ,
,
所以![]() 是奇函数,
是奇函数,
所以不等式![]() 可变为
可变为![]() ,
,
由(1)知![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,
,
解得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列五个结论,其中正确的结论是( )
A.函数
 的最大值为
的最大值为
B.已知函数
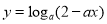 (
( 且
且 )在
)在 上是减函数则a的取值范围是
上是减函数则a的取值范围是
C.在同一直角坐标系中,函数
 与
与 的图象关于y轴对称
的图象关于y轴对称D.在同一直角坐标系中,函数
 与
与 的图象关于直线
的图象关于直线 对称
对称E.已知定义在R上的奇函数
 在
在 内有1010个零点,则函数
内有1010个零点,则函数 的零点个数为2021
的零点个数为2021 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 (
( )与抛物线
)与抛物线 (
( )共交点
)共交点 ,抛物线上的点
,抛物线上的点 到
到 轴的距离等于
轴的距离等于 ,且椭圆与抛物线的交点
,且椭圆与抛物线的交点 满足
满足 .
.(1)求抛物线的方程和椭圆的方程;
(2)国抛物线上的点
 做抛物线的切线
做抛物线的切线 交椭圆于
交椭圆于 两点,设线段
两点,设线段 的中点为
的中点为 ,求
,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某种热饮需用开水冲泡,其基本操作流程如下:①先将水加热到100
 ,水温
,水温 与时间
与时间 近似满足一次函数关系;②用开水将热饮冲泡后在室温下放置,温度
近似满足一次函数关系;②用开水将热饮冲泡后在室温下放置,温度 与时间
与时间 近似满足函数的关系式为
近似满足函数的关系式为  (
( 为常数), 通常这种热饮在40
为常数), 通常这种热饮在40 时,口感最佳,某天室温为
时,口感最佳,某天室温为 时,冲泡热饮的部分数据如图所示,那么按上述流程冲泡一杯热饮,并在口感最佳时饮用,最少需要的时间为
时,冲泡热饮的部分数据如图所示,那么按上述流程冲泡一杯热饮,并在口感最佳时饮用,最少需要的时间为
A. 35
 B. 30
B. 30
C. 25
 D. 20
D. 20
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,直线
中,直线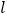 经过点
经过点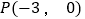 ,其倾斜角为
,其倾斜角为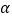 ,以原点
,以原点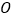 为极点,以
为极点,以 轴为非负半轴为极轴,与坐标系
轴为非负半轴为极轴,与坐标系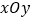 取相同的长度单位,建立极坐标系.设曲线
取相同的长度单位,建立极坐标系.设曲线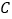 的极坐标方程为
的极坐标方程为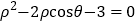 .
.(1)若直线
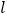 与曲线
与曲线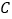 有公共点,求倾斜角
有公共点,求倾斜角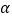 的取值范围;
的取值范围;(2)设
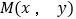 为曲线
为曲线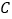 上任意一点,求
上任意一点,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面使用类比推理,得到的结论正确的是( )
A. 直线
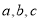 ,若
,若 ,则
,则 .类比推出:向量
.类比推出:向量 ,
, ,
, ,若
,若 ∥
∥ ,
, ∥
∥ ,则
,则 ∥
∥ .
.B. 三角形的面积为
 ,其中
,其中 ,
, ,
, 为三角形的边长,
为三角形的边长, 为三角形内切圆的半径,类比推出,可得出四面体的体积为
为三角形内切圆的半径,类比推出,可得出四面体的体积为 ,(
,( ,
, ,
, ,
, 分别为四面体的四个面的面积,
分别为四面体的四个面的面积, 为四面体内切球的半径)
为四面体内切球的半径)C. 同一平面内,直线
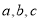 ,若
,若 ,则
,则 .类比推出:空间中,直线
.类比推出:空间中,直线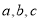 ,若
,若 ,则
,则 .
.D. 实数
 ,若方程
,若方程 有实数根,则
有实数根,则 .类比推出:复数
.类比推出:复数 ,若方程
,若方程 有实数根,则
有实数根,则 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, ,其中
,其中 ,(
,( ).
).(1)若函数
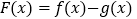 有极值
有极值 ,求
,求 的值;
的值;(2)若函数
 在区间
在区间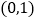 上为减函数,求
上为减函数,求 的取值范围;
的取值范围;(3)证明:
 .
.
相关试题

