【题目】[选修4-4:坐标系与参数方程]:在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() ,
,![]() 的直角坐标方程;
的直角坐标方程;
(2)判断曲线![]() ,
,![]() 是否相交,若相交,请求出交点间的距离;若不相交,请说明理由.
是否相交,若相交,请求出交点间的距离;若不相交,请说明理由.
参考答案:
【答案】(1)![]() ;
; ![]() (2)
(2)![]()
【解析】
(1)由题意,消去参数,即可得到曲线![]() 的直角坐标方程,再利用极坐标与直角坐标的互化,即可得到曲线
的直角坐标方程,再利用极坐标与直角坐标的互化,即可得到曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)由(1),将![]() 代入曲线
代入曲线![]() ,求得
,求得![]() ,
,![]() ,在由曲线
,在由曲线![]() ,
,![]() 两交点间的距离公式,即可求解。
两交点间的距离公式,即可求解。
(1)将![]() ,消去参数,得曲线
,消去参数,得曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
将![]() 展开整理,得
展开整理,得![]() ,
,
因为![]() ,
,![]() ,
,
所以曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)由(1)知曲线![]() 是过定点
是过定点![]() 的直线,因为点
的直线,因为点![]() 在曲线
在曲线![]() 的内部,所以曲线
的内部,所以曲线![]() 与曲线
与曲线![]() 相交.将
相交.将![]() 代入
代入![]() 并整理,得
并整理,得![]() ,
,
设曲线![]() ,
,![]() 的两交点为
的两交点为![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
故曲线![]() ,
,![]() 两交点间的距离
两交点间的距离![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
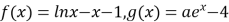 (
(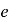 为自然对数的底数,
为自然对数的底数,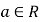 ).
).(1)求函数
 在点
在点 处的切线方程;
处的切线方程;(2)若对于任意
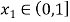 ,存在
,存在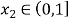 ,使得
,使得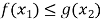 ,求
,求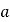 的取值范围;
的取值范围;(3)若
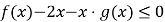 恒成立,求
恒成立,求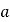 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点
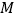 在正视图上的对应点为
在正视图上的对应点为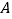 ,圆柱表面上的点
,圆柱表面上的点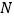 在左视图上的对应点为
在左视图上的对应点为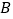 ,则在此圆柱侧面上,从
,则在此圆柱侧面上,从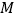 到
到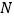 的路径中,最短路径的长度为( )
的路径中,最短路径的长度为( )
A.
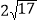 B.
B. 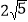 C.
C. 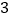 D. 2
D. 2 -
科目: 来源: 题型:
查看答案和解析>>【题目】设
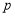 :实数
:实数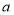 满足不等式
满足不等式 ,
,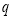 :函数
:函数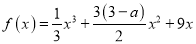 无极值点.
无极值点.(1)若“
 ”为假命题,“
”为假命题,“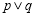 ”为真命题,求实数
”为真命题,求实数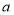 的取值范围;
的取值范围;(2)若“
 为真命题”是“
为真命题”是“ ”的必要不充分条件,求正整数
”的必要不充分条件,求正整数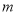 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为
 =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(
 ,
, )
)C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题14分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(
 吨)与相应的生产能耗
吨)与相应的生产能耗 (吨)标准煤的几组对照数据:
(吨)标准煤的几组对照数据:
3
4
5
6

2.5
3
4
4.5

(1)请画出上表数据的散点图;并指出x,y 是否线性相关;
(2)请根据上表提供的数据,用最小二乘法求出
 关于
关于 的线性回归方程
的线性回归方程 ;
;(3)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考:用最小二乘法求线性回归方程系数公式
 ,
, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】一汽车厂生产
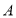 ,
,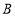 ,
, 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有
三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有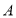 类轿车10辆.
类轿车10辆.轿车
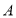
轿车
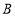
轿车

舒适型
100
150
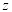
标准型
300
450
600
(1)求
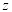 的值;
的值;(2)用分层抽样的方法在
 类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;(3)用随机抽样的方法从
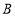 类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2 把这8辆轿车的得分看作一个总体,从中任取一个得分数
类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2 把这8辆轿车的得分看作一个总体,从中任取一个得分数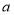 ,记这8辆轿车的得分的平均数为
,记这8辆轿车的得分的平均数为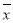 ,定义事件
,定义事件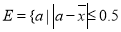 ,且函数
,且函数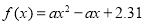 没有零点
没有零点 ,求事件
,求事件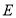 发生的概率.
发生的概率.
相关试题

