【题目】(本题14分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(![]() 吨)与相应的生产能耗
吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据:
(吨)标准煤的几组对照数据:
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |

(1)请画出上表数据的散点图;并指出x,y 是否线性相关;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考:用最小二乘法求线性回归方程系数公式 ,
,![]() )
)
参考答案:
【答案】(1)见解析.(2)![]() .(3)
.(3)![]() 吨.
吨.
【解析】
求回归直线方程的方法是较多的,既有最常用的“最小二乘法”,又有简便易行的计算器法,还有用计算机软件来完成的方法,同时应注意:两个变量具有相关关系是回归分析的前提;求回归直线方程,首先应注意到,只有在散点图大至呈线性时,求出的回归直线方程才有实际意义,否则,求出的回归直线方程毫无意义.
利用回归分析的方法对两个具有线性相关关系的变量研究的步骤为:(1)画出这两个变量的散点图;(2)求回归直线方程;(3)利用回归直线方程进行预报
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有
 (n≥2,n∈N*)个给定的不同的数随机排成一个下图所示的三角形数阵:
(n≥2,n∈N*)个给定的不同的数随机排成一个下图所示的三角形数阵: 
设Mk是第k行中的最大数,其中1≤k≤n,k∈N*.记M1<M2<…<Mn的概率为pn .
(1)求p2的值;
(2)证明:pn> .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某运动员每次投篮命中的概率等于
 .现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0,表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0,表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校艺术节对同一类的
 ,
, ,
, ,
, 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:甲说:“是
 或
或 作品获得一等奖”;
作品获得一等奖”;乙说:“
 作品获得一等奖”;
作品获得一等奖”;丙说:“
 ,
, 两项作品未获得一等奖”;
两项作品未获得一等奖”;丁说:“是
 作品获得一等奖”.
作品获得一等奖”.若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】高三年级有500名学生,为了了解数学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
分组
频数
频率








12
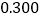



4



合计

 根据上面图表,求
根据上面图表,求 处的数值
处的数值 在所给的坐标系中画出
在所给的坐标系中画出 的频率分布直方图;
的频率分布直方图; 根据题中信息估计总体平均数,并估计总体落在
根据题中信息估计总体平均数,并估计总体落在 中的概率.
中的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 图像上有一最低点
图像上有一最低点 ,若图像上各点纵坐标不变,横坐标缩为原来的
,若图像上各点纵坐标不变,横坐标缩为原来的 倍,再向左平移
倍,再向左平移 个单位得
个单位得 ,又
,又 的所有根从小到大依次相差
的所有根从小到大依次相差 个单位,则
个单位,则 的解析式为__________.
的解析式为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
(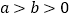 ,
, 为参数),在以
为参数),在以 为极点,
为极点, 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线 是圆心在极轴上,且经过极点的圆.已知曲线
是圆心在极轴上,且经过极点的圆.已知曲线 上的点
上的点 对应的参数
对应的参数 ,射线
,射线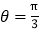 与曲线
与曲线 交于点
交于点 .
.(Ⅰ)求曲线
 ,
, 的标准方程;
的标准方程;(Ⅱ)若点
 ,
, 在曲线
在曲线 上,求
上,求 的值.
的值.
相关试题

