【题目】如图,在△ABC中,∠BAC=90°,PA⊥面ABC,AB=AC,D是BC的中点,则图中直角三角形的个数是 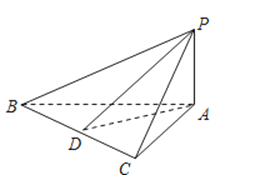
参考答案:
【答案】8
【解析】解:在Rt△ABC中,∠BAC=90°,
PA⊥平面ABC,
∴AB⊥PA,PA⊥DA,PA⊥AC,
∵AB=AC,D是BC的中点,
∴AD⊥BC,
∴BP=CP,可得PD⊥BC,
∴图中直角三角形有△PAC,△PAB,△PAD,△ABC.△ABD,△ADC,△BPD,△DPC,8个.
所以答案是:8.
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,
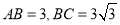 ,点E,H分别是所在边靠近B,D的三等分点,现沿着EH将矩形折成直二面角,分别连接AD,AC,CB,形成如图所示的多面体.
,点E,H分别是所在边靠近B,D的三等分点,现沿着EH将矩形折成直二面角,分别连接AD,AC,CB,形成如图所示的多面体.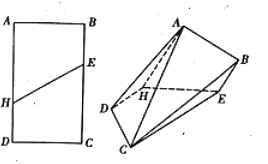
(1)证明:平面BCE∥平面ADH;
(2)证明:EH⊥AC;
(3)求二面角B-AC-D的平面角的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD为正方形,PD⊥平面ABCD且PD=AD,则下列命题中错误的是( )
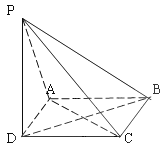
A.过BD且与PC平行的平面交PA于M点,则M为PA的中点
B.过AC且与PB垂直的平面交PB于N点,则N为PB的中点
C.过AD且与PC垂直的平面交PC于H点,则H为PC的中点
D.过P、B、C的平面与平面PAD的交线为直线l,则l∥AD -
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形ABCD的边AB=a,BC=3,PA⊥平面ABCD,若BC边上有且只有一点M,使PM⊥DM,则a的值为
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面
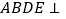 平面
平面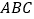 ,
,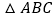 是等腰直角三角形,
是等腰直角三角形,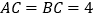 ,四边形
,四边形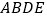 是直角梯形,
是直角梯形,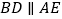 ,
,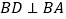 ,
,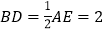 ,
, ,
,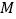 分别为
分别为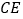 ,
,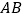 的中点.
的中点.(I)求证:
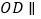 平面
平面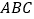 .
.(II)求直线
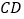 和平面
和平面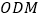 所成角的正弦值.
所成角的正弦值.(III)能否在
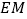 上找一点
上找一点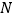 ,使得
,使得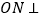 平面
平面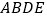 ?若能,请指出点
?若能,请指出点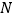 的位置,并加以证明;若不能,请说明理由.
的位置,并加以证明;若不能,请说明理由.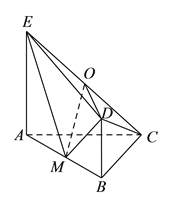
-
科目: 来源: 题型:
查看答案和解析>>【题目】三棱锥S﹣ABC中,SA⊥AB,SA⊥AC,AC⊥BC且AC=2,BC=
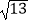 , SB=
, SB=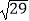 .
.
(1)证明:SC⊥BC;
(2)求三棱锥的体积VS﹣ABC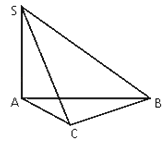
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=6,BD=8,E是PB上任意一点,△AEC面积的最小值是3.
(Ⅰ)求证:AC⊥DE;
(Ⅱ)求四棱锥P﹣ABCD的体积.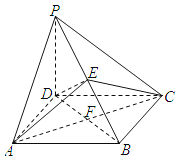
相关试题

