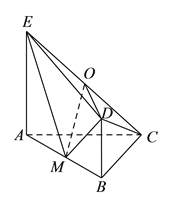
【题目】如图,平面![]() 平面
平面![]() ,
,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,四边形
,四边形![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
(I)求证:![]() 平面
平面![]() .
.
(II)求直线![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
(III)能否在![]() 上找一点
上找一点![]() ,使得
,使得![]() 平面
平面![]() ?若能,请指出点
?若能,请指出点![]() 的位置,并加以证明;若不能,请说明理由.
的位置,并加以证明;若不能,请说明理由.
参考答案:
【答案】(I)见解析;(II)![]() ;(III)见解析.
;(III)见解析.
【解析】试题分析:(1)先建立空间直角坐标系,利用法向量证明OD//平面ABC,说明![]() 和平面ABC的法向量
和平面ABC的法向量![]() 垂直即可;(2)设直线CD与平面ODM所成角为θ,求出平面ODM法向量
垂直即可;(2)设直线CD与平面ODM所成角为θ,求出平面ODM法向量![]() ,则
,则 ;(3)设EM上一点N满足,
;(3)设EM上一点N满足,![]() 平面ABDE法向量
平面ABDE法向量![]() ,
,![]() 不存在
不存在![]() 使
使![]() ∴ 不存在满足题意的点N.
∴ 不存在满足题意的点N.
试题解析:以B为原点,BC为x轴,BA为y轴,BD为z轴,建立空间直角坐标系
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)平面ABC的法向量![]() ,
,![]() ,
,![]()
∴OD//平面ABC
(2)设平面ODM法向量为![]() ,直线CD与平面ODM所成角为θ
,直线CD与平面ODM所成角为θ
![]() ,
,![]() ,∴
,∴![]() ,
,![]()
∴ .
.
(3)设EM上一点N满足,![]()
平面ABDE法向量![]() ,
,![]()
不存在![]() 使
使![]() ∴不存在满足题意的点N.
∴不存在满足题意的点N.
(传统方法参照给分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD为正方形,PD⊥平面ABCD且PD=AD,则下列命题中错误的是( )
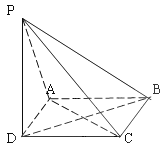
A.过BD且与PC平行的平面交PA于M点,则M为PA的中点
B.过AC且与PB垂直的平面交PB于N点,则N为PB的中点
C.过AD且与PC垂直的平面交PC于H点,则H为PC的中点
D.过P、B、C的平面与平面PAD的交线为直线l,则l∥AD -
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形ABCD的边AB=a,BC=3,PA⊥平面ABCD,若BC边上有且只有一点M,使PM⊥DM,则a的值为
-
科目: 来源: 题型:
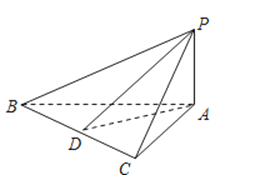
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,PA⊥面ABC,AB=AC,D是BC的中点,则图中直角三角形的个数是
-
科目: 来源: 题型:
查看答案和解析>>【题目】三棱锥S﹣ABC中,SA⊥AB,SA⊥AC,AC⊥BC且AC=2,BC=
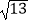 , SB=
, SB=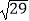 .
.
(1)证明:SC⊥BC;
(2)求三棱锥的体积VS﹣ABC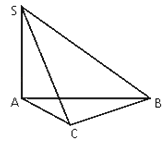
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=6,BD=8,E是PB上任意一点,△AEC面积的最小值是3.
(Ⅰ)求证:AC⊥DE;
(Ⅱ)求四棱锥P﹣ABCD的体积.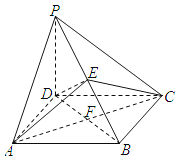
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥P﹣ABC中,AB⊥平面PAC,∠APC=90°,E是AB的中点,M是CE的中点,N点在PB上,且4PN=PB.
(Ⅰ)证明:平面PCE⊥平面PAB;
(Ⅱ)证明:MN∥平面PAC.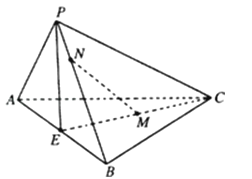
相关试题

