【题目】如图,已知四边形ABCD为正方形,PD⊥平面ABCD且PD=AD,则下列命题中错误的是( )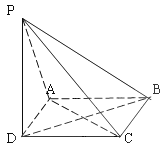
A.过BD且与PC平行的平面交PA于M点,则M为PA的中点
B.过AC且与PB垂直的平面交PB于N点,则N为PB的中点
C.过AD且与PC垂直的平面交PC于H点,则H为PC的中点
D.过P、B、C的平面与平面PAD的交线为直线l,则l∥AD
参考答案:
【答案】B
【解析】解:设AC∩BD=O,∵ABCD是正方形,∴O是AC中点,
∵过BD且与PC平行的平面交PA于M点,∴OM∥PC,
∴M是PA中点,故A正确;
设N为PB的中点,连结AN,
∵PA与AB不一定相等,∴AN与PB不一定垂直,
∴过AC且与PB垂直的平面交PB于N点,则N不一定是PB中点,故B错误;
∵四边形ABCD为正方形,PD⊥平面ABCD且PD=AD,
∴PA=AC,PD=DC,
∴过AD且与PC垂直的平面宛PC于H点,则H为PC的中点,故C正确;
∵AD∥BC,平面PAD与平面PCB有公共点P,
∴l∥AD∥BC,故D正确.
故选:B.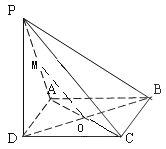
【考点精析】本题主要考查了直线与平面垂直的性质的相关知识点,需要掌握垂直于同一个平面的两条直线平行才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方体
 的棱长为
的棱长为 ,
,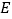 ,
,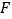 分别是棱
分别是棱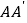 ,
,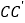 的中点,过直线
的中点,过直线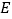 ,
,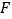 的平面分别与棱
的平面分别与棱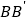 、
、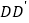 交于
交于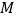 ,
,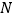 ,设
,设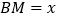 ,
,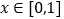 ,给出以下四个命题:
,给出以下四个命题:①平面
 平面
平面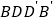 ;
;②当且仅当
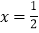 时,四边形
时,四边形 的面积最小;
的面积最小;③四边形
 周长
周长 ,
,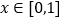 是单调函数;
是单调函数;④四棱锥
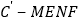 的体积
的体积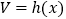 为常函数;
为常函数;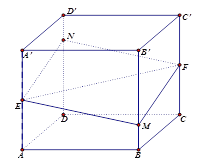
以上命题中假命题的序号为( ).
A. ①④ B. ② C. ③ D. ③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠DAB=60°.侧面PAD为正三角形,且平面PAD⊥平面ABCD,则下列说法错误的是( )
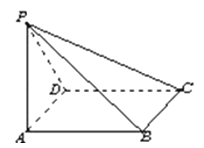
A.在棱AD上存在点M,使AD⊥平面PMB
B.异面直线AD与PB所成的角为90°
C.二面角P﹣BC﹣A的大小为45°
D.BD⊥平面PAC -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,
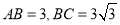 ,点E,H分别是所在边靠近B,D的三等分点,现沿着EH将矩形折成直二面角,分别连接AD,AC,CB,形成如图所示的多面体.
,点E,H分别是所在边靠近B,D的三等分点,现沿着EH将矩形折成直二面角,分别连接AD,AC,CB,形成如图所示的多面体.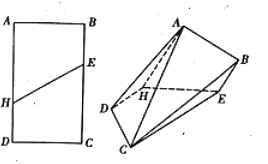
(1)证明:平面BCE∥平面ADH;
(2)证明:EH⊥AC;
(3)求二面角B-AC-D的平面角的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形ABCD的边AB=a,BC=3,PA⊥平面ABCD,若BC边上有且只有一点M,使PM⊥DM,则a的值为
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,PA⊥面ABC,AB=AC,D是BC的中点,则图中直角三角形的个数是
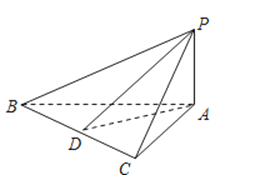
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面
 平面
平面 ,
,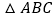 是等腰直角三角形,
是等腰直角三角形,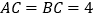 ,四边形
,四边形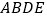 是直角梯形,
是直角梯形,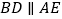 ,
,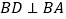 ,
,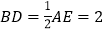 ,
, ,
,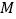 分别为
分别为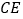 ,
,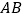 的中点.
的中点.(I)求证:
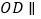 平面
平面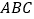 .
.(II)求直线
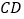 和平面
和平面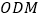 所成角的正弦值.
所成角的正弦值.(III)能否在
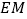 上找一点
上找一点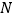 ,使得
,使得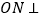 平面
平面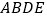 ?若能,请指出点
?若能,请指出点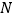 的位置,并加以证明;若不能,请说明理由.
的位置,并加以证明;若不能,请说明理由.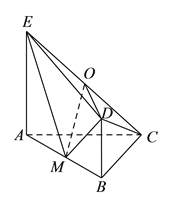
相关试题

