【题目】如图,在矩形ABCD中, ![]() ,点E,H分别是所在边靠近B,D的三等分点,现沿着EH将矩形折成直二面角,分别连接AD,AC,CB,形成如图所示的多面体.
,点E,H分别是所在边靠近B,D的三等分点,现沿着EH将矩形折成直二面角,分别连接AD,AC,CB,形成如图所示的多面体.
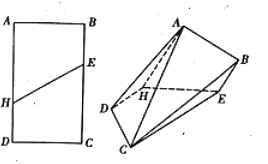
(1)证明:平面BCE∥平面ADH;
(2)证明:EH⊥AC;
(3)求二面角B-AC-D的平面角的余弦值.
参考答案:
【答案】(1)见解析(2)![]() .
.
【解析】试题分析:(1)根据折叠前、后不变量得AH∥BE,DH∥EC,根据线面平行判定定理得AH∥平面BCE,DH∥平面BCE,再根据面面平行判定定理得平面BCE∥平面ADH.(2)先过点A作EH的垂线交EH于点O,由面面垂直性质定理得AO⊥平面EHC,再由直二面角定义得CO⊥EH,因此根据线面垂直判定定理得EH⊥平面AOC,即得EH⊥AC.(3)根据条件作出二面角B-AC-O平面角![]() BQP,并根据直角三角形求出
BQP,并根据直角三角形求出![]() ,最后根据二面角B-AC-D的平面角为
,最后根据二面角B-AC-D的平面角为![]() BQP,并利用二倍角余弦公式求值.
BQP,并利用二倍角余弦公式求值.
试题解析:(1)证明:由折叠前、后图形对比可知,在矩形ABCD中有AH∥BE,DH∥EC,
又∵AH∩DH=H,BE∩CE=E,∴平面BCE∥平面ADH.
(2)证明:在多面体中,过点A作EH的垂线交EH于点O,连接OC.
∵二面角A-EH-C为直二面角,∴AO⊥平面EHC.
由对称性可知CO⊥EH,又AO∩CO=O.
∴EH⊥平面AOC,而![]() 平面AOC,∴EH⊥AC.
平面AOC,∴EH⊥AC.
(3)解:过点B在平面ABEH内作BP⊥AO垂足为P,过点P在平面AOC内作PQ⊥AC垂足为Q,连接BQ.∵△ABO是边长为3的等边三角形,∴点P为中点, ![]() .
.
∵△AOC是直角边长为3的等腰直角三角形![]() ,∴
,∴![]() .
.
又∵CO⊥平面ABEH,∴CO⊥BP,BP⊥AO,AO∩CO=O,∴BP⊥平面AOC.
∴![]() BQP为二面角B-AC-O的平面角,在直角三角形BPQ中
BQP为二面角B-AC-O的平面角,在直角三角形BPQ中![]() ,
,
∴![]() .
.
设二面角B-AC-D的平面角为![]() ,∴
,∴![]() .
.
所以二面角B-AC-D的平面角的余弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年春节,“抢红包”成为社会热议的话题之一.某机构对春节期间用户利用手机“抢红包”的情况进行调查,如果一天内抢红包的总次数超过10次为“关注点高”,否则为“关注点低”,调查情况如下表所示:

(1)填写上表中x,y的值并判断是否有95%以上的把握认为性别与关注点高低有关?
(2)现要从上述男性用户中随机选出3名参加一项活动,以X表示选中的同学中抢红包总次数超过10次的人数,求随机变量X的分布列及数学期望E(X).
下面的临界值表供参考:

独立性检验统计量
 ,其中n=a+b+c+d.
,其中n=a+b+c+d. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正方体
 的棱长为
的棱长为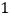 ,
,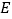 ,
,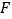 分别是棱
分别是棱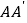 ,
,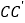 的中点,过直线
的中点,过直线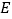 ,
,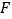 的平面分别与棱
的平面分别与棱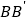 、
、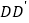 交于
交于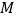 ,
,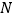 ,设
,设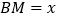 ,
,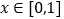 ,给出以下四个命题:
,给出以下四个命题:①平面
 平面
平面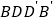 ;
;②当且仅当
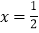 时,四边形
时,四边形 的面积最小;
的面积最小;③四边形
 周长
周长 ,
,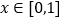 是单调函数;
是单调函数;④四棱锥
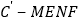 的体积
的体积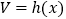 为常函数;
为常函数;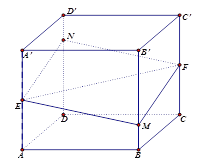
以上命题中假命题的序号为( ).
A. ①④ B. ② C. ③ D. ③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠DAB=60°.侧面PAD为正三角形,且平面PAD⊥平面ABCD,则下列说法错误的是( )
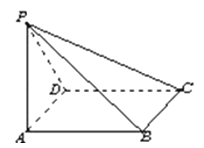
A.在棱AD上存在点M,使AD⊥平面PMB
B.异面直线AD与PB所成的角为90°
C.二面角P﹣BC﹣A的大小为45°
D.BD⊥平面PAC -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD为正方形,PD⊥平面ABCD且PD=AD,则下列命题中错误的是( )
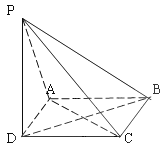
A.过BD且与PC平行的平面交PA于M点,则M为PA的中点
B.过AC且与PB垂直的平面交PB于N点,则N为PB的中点
C.过AD且与PC垂直的平面交PC于H点,则H为PC的中点
D.过P、B、C的平面与平面PAD的交线为直线l,则l∥AD -
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形ABCD的边AB=a,BC=3,PA⊥平面ABCD,若BC边上有且只有一点M,使PM⊥DM,则a的值为
-
科目: 来源: 题型:
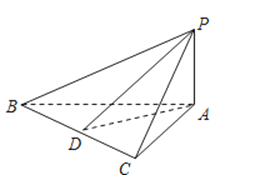
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,PA⊥面ABC,AB=AC,D是BC的中点,则图中直角三角形的个数是
相关试题

