【题目】如图,AB为圆O的直径,C在圆O上,CF⊥AB于F,点D为线段CF上任意一点,延长AD交圆O于E,∠AEC=30°. 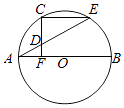
(1)求证:AF=FO;
(2)若CF= ![]() ,求ADAE的值.
,求ADAE的值.
参考答案:
【答案】
(1)证明:连接OC,AC,
∵∠AEC=30°,
∴∠AOC=60°.
∵OA=OC,
∴△AOC为等边三角形.
∵CF⊥AB,
∴CF为△AOC中AO边上的中线,即AF=FO
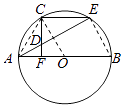
(2)解:连接BE,
∵CF= ![]() ,△AOC为等边三角形,∴AF=1,AB=4.
,△AOC为等边三角形,∴AF=1,AB=4.
∵AB是圆O的直径,∴∠AEB=90°,∴∠AEB=∠AFD.
∴B,E,D,F四点共圆
∴ADAE=ABAF=4
【解析】(1)连接OC,AC,证明△AOC为等边三角形,利用CF⊥AB,得出CF为△AOC中AO边上的中线,即可证明结论;(2)证明B,E,D,F四点共圆,利用割线定理,求ADAE的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
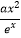 ,直线y=
,直线y= 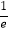 x为曲线y=f(x)的切线(e为自然对数的底数).
x为曲线y=f(x)的切线(e为自然对数的底数).
(1)求实数a的值;
(2)用min{m,n}表示m,n中的最小值,设函数g(x)=min{f(x),x﹣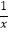 }(x>0),若函数h(x)=g(x)﹣cx2为增函数,求实数c的取值范围.
}(x>0),若函数h(x)=g(x)﹣cx2为增函数,求实数c的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在棱锥
 中,侧面
中,侧面 是边长为2的正三角形,底面
是边长为2的正三角形,底面 是菱形,且
是菱形,且 ,
, 为
为 的中点,二面角
的中点,二面角 为
为 .
.
(1)求证:
 平面
平面 ;
;(2)求二面角
 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
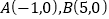 ,若在圆
,若在圆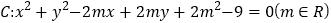 上存在点
上存在点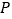 使得
使得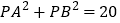 成立,则
成立,则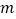 的取值范围为_____.
的取值范围为_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】
 的内角
的内角 的对边分别为
的对边分别为 ,已知
,已知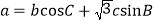 .
.(1)求
 ;
;(2)若
 ,求
,求 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系中x轴的正半轴重合,若曲线C的参数方程为
 (α是参数),直线l的极坐标方程为
(α是参数),直线l的极坐标方程为  ρsin(θ﹣
ρsin(θ﹣  )=1.
)=1.
(1)将曲线C的参数方程化为极坐标方程;
(2)由直线l上一点向曲线C引切线,求切线长的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的不等式|x﹣2|﹣|x+3|≥|m+1|有解,记实数m的最大值为M.
(1)求M的值;
(2)正数a,b,c满足a+2b+c=M,求证: +
+  ≥1.
≥1.
相关试题

