【题目】已知函数f(x)= ![]() ,直线y=
,直线y= ![]() x为曲线y=f(x)的切线(e为自然对数的底数).
x为曲线y=f(x)的切线(e为自然对数的底数).
(1)求实数a的值;
(2)用min{m,n}表示m,n中的最小值,设函数g(x)=min{f(x),x﹣ ![]() }(x>0),若函数h(x)=g(x)﹣cx2为增函数,求实数c的取值范围.
}(x>0),若函数h(x)=g(x)﹣cx2为增函数,求实数c的取值范围.
参考答案:
【答案】
(1)解:函数f(x)= ![]() 的导数为f′(x)=
的导数为f′(x)= ![]() ,
,
设切点为(m,n),即有n= ![]() ,n=
,n= ![]() m,
m,
可得ame=em,①
由直线y= ![]() x为曲线y=f(x)的切线,可得
x为曲线y=f(x)的切线,可得
![]() =
= ![]() ,②
,②
由①②解得m=1,a=1
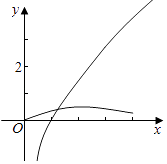
(2)解:函数g(x)=min{f(x),x﹣ ![]() }(x>0),
}(x>0),
由f(x)= ![]() 的导数为f′(x)=
的导数为f′(x)= ![]() ,
,
当0<x<2时,f(x)递增,x>2时,f(x)递减.
对x﹣ ![]() 在x>0递增,设y=f(x)和y=x﹣
在x>0递增,设y=f(x)和y=x﹣ ![]() 的交点为(x0,y0),
的交点为(x0,y0),
由f(1)﹣(1﹣1)= ![]() >0,f(2)﹣(2﹣
>0,f(2)﹣(2﹣ ![]() )=
)= ![]() ﹣
﹣ ![]() <0,即有1<x0<2,
<0,即有1<x0<2,
当0<x<x0时,g(x)=x﹣ ![]() ,
,
h(x)=g(x)﹣cx2=x﹣ ![]() ﹣cx2,h′(x)=1+
﹣cx2,h′(x)=1+ ![]() ﹣2cx,
﹣2cx,
由题意可得h′(x)≥0在0<x<x0时恒成立,
即有2c≤ ![]() +
+ ![]() ,由y=
,由y= ![]() +
+ ![]() 在(0,x0)递减,
在(0,x0)递减,
可得2c≤ ![]() +
+ ![]() ①
①
当x≥x0时,g(x)= ![]() ,
,
h(x)=g(x)﹣cx2= ![]() ﹣cx2,h′(x)=
﹣cx2,h′(x)= ![]() ﹣2cx,
﹣2cx,
由题意可得h′(x)≥0在x≥x0时恒成立,
即有2c≤ ![]() ,由y=
,由y= ![]() ,可得y′=
,可得y′= ![]() ,
,
可得函数y在(3,+∞)递增;在(x0,3)递减,
即有x=3处取得极小值,且为最小值﹣ ![]() .
.
可得2c≤﹣ ![]() ②,
②,
由①②可得2c≤﹣ ![]() ,解得c≤﹣
,解得c≤﹣ ![]() .
.
【解析】(1)求出f(x)的导数,设出切点(m,n),可得切线的斜率,由切线方程可得a,m的方程,解方程可得a=1;(2)y=f(x)和y=x﹣ ![]() 的交点为(x0 , y0),分别画出y=f(x)和y=x﹣
的交点为(x0 , y0),分别画出y=f(x)和y=x﹣ ![]() 在x>0的图象,可得1<x0<2,再由新定义求得最小值,求得h(x)的解析式,由题意可得h′(x)≥0在0<x<x0时恒成立,运用参数分离和函数的单调性,即可得到所求c的范围.
在x>0的图象,可得1<x0<2,再由新定义求得最小值,求得h(x)的解析式,由题意可得h′(x)≥0在0<x<x0时恒成立,运用参数分离和函数的单调性,即可得到所求c的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某中学高中某学科竞赛中,该中学100名考生的参赛成绩统计如图所示.

(1)求这100名考生的竞赛平均成绩(同一组中数据用该组区间中点作代表);
(2)记70分以上为优秀,70分及以下为合格,结合频率分布直方图完成下表,并判断是否有99%的把握认为该学科竞赛成绩与性别有关?
合格
优秀
合计
男生
18
女生
25
合计
100
附:
 .
.
0.050
0.010
0.005

3.841
6.635
7.879
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知过点A(0,2)的直线
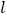 与椭圆C:
与椭圆C: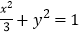 交于P,Q两点.
交于P,Q两点.(1)若直线
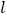 的斜率为k,求k的取值范围;
的斜率为k,求k的取值范围;(2)若以PQ为直径的圆经过点E(1,0),求直线
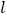 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在正方体
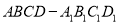 中,点
中,点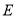 是棱
是棱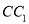 上的一个动点,平面
上的一个动点,平面 交棱
交棱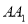 于点
于点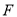 .给出下列命题:
.给出下列命题: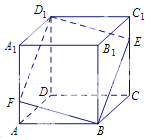
①存在点
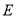 ,使得
,使得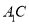 //平面
//平面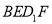 ;
;②对于任意的点
 ,平面
,平面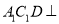 平面
平面 ;
;③存在点
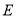 ,使得
,使得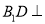 平面
平面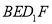 ;
;④对于任意的点
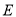 ,四棱锥
,四棱锥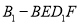 的体积均不变.
的体积均不变.其中正确命题的序号是______.(写出所有正确命题的序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在棱锥
 中,侧面
中,侧面 是边长为2的正三角形,底面
是边长为2的正三角形,底面 是菱形,且
是菱形,且 ,
, 为
为 的中点,二面角
的中点,二面角 为
为 .
.
(1)求证:
 平面
平面 ;
;(2)求二面角
 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
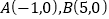 ,若在圆
,若在圆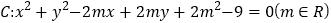 上存在点
上存在点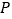 使得
使得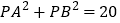 成立,则
成立,则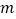 的取值范围为_____.
的取值范围为_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为圆O的直径,C在圆O上,CF⊥AB于F,点D为线段CF上任意一点,延长AD交圆O于E,∠AEC=30°.
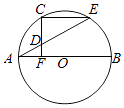
(1)求证:AF=FO;
(2)若CF= ,求ADAE的值.
,求ADAE的值.
相关试题

