【题目】已知![]() ,若在圆
,若在圆![]() 上存在点
上存在点![]() 使得
使得![]() 成立,则
成立,则![]() 的取值范围为_____.
的取值范围为_____.
参考答案:
【答案】![]() 或
或![]()
【解析】
先由PA2+PB2=20得P点轨迹为圆,然后问题转化为两圆有交点,圆心距小于等于半径之和,大于等于半径之差.
:∵圆C:(x-m)2+(y+m)2=9,∴圆心为C(m,-m),半径为3,设P(x,y),则由PA2+PB2=20,得(x+1)2+y2+(x-5)2+y2=20,即x2+y2-4x+3=0,∴(x-2)2+y2=1,在圆C:x2+y2-2mx+2my+2m2-9=0(m∈R)上存在点P使得PA2+PB2=20成立,转化为:圆C:
(x-m)2+(x+m)2=9与圆:(x-2)2+y2=1有交点,转化为:圆心距小于等于两圆半径之和,大于等于两圆半径之差,即3-1≤![]() ≤3+1,解得:-2≤m≤0或2≤m≤3.
≤3+1,解得:-2≤m≤0或2≤m≤3.
故答案为:-2≤m≤0或2≤m≤3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在正方体
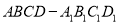 中,点
中,点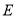 是棱
是棱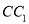 上的一个动点,平面
上的一个动点,平面 交棱
交棱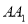 于点
于点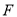 .给出下列命题:
.给出下列命题:
①存在点
 ,使得
,使得 //平面
//平面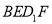 ;
;②对于任意的点
 ,平面
,平面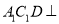 平面
平面 ;
;③存在点
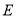 ,使得
,使得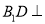 平面
平面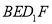 ;
;④对于任意的点
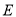 ,四棱锥
,四棱锥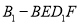 的体积均不变.
的体积均不变.其中正确命题的序号是______.(写出所有正确命题的序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
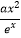 ,直线y=
,直线y= 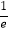 x为曲线y=f(x)的切线(e为自然对数的底数).
x为曲线y=f(x)的切线(e为自然对数的底数).
(1)求实数a的值;
(2)用min{m,n}表示m,n中的最小值,设函数g(x)=min{f(x),x﹣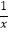 }(x>0),若函数h(x)=g(x)﹣cx2为增函数,求实数c的取值范围.
}(x>0),若函数h(x)=g(x)﹣cx2为增函数,求实数c的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在棱锥
 中,侧面
中,侧面 是边长为2的正三角形,底面
是边长为2的正三角形,底面 是菱形,且
是菱形,且 ,
, 为
为 的中点,二面角
的中点,二面角 为
为 .
.
(1)求证:
 平面
平面 ;
;(2)求二面角
 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为圆O的直径,C在圆O上,CF⊥AB于F,点D为线段CF上任意一点,延长AD交圆O于E,∠AEC=30°.
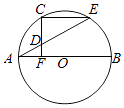
(1)求证:AF=FO;
(2)若CF= ,求ADAE的值.
,求ADAE的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】
 的内角
的内角 的对边分别为
的对边分别为 ,已知
,已知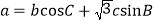 .
.(1)求
 ;
;(2)若
 ,求
,求 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系中x轴的正半轴重合,若曲线C的参数方程为
 (α是参数),直线l的极坐标方程为
(α是参数),直线l的极坐标方程为  ρsin(θ﹣
ρsin(θ﹣  )=1.
)=1.
(1)将曲线C的参数方程化为极坐标方程;
(2)由直线l上一点向曲线C引切线,求切线长的最小值.
相关试题

