【题目】已知![]() 是二次函数,不等式
是二次函数,不等式![]() 的解集是
的解集是![]() ,且
,且![]() 在区间
在区间![]() 上的最大值是12.
上的最大值是12.
(1)求![]() 的解析式;
的解析式;
(2)是否存在自然数![]() ,使得方程
,使得方程![]() 在区间
在区间![]() 内有且只有两个不等的实数根?若存在,求出
内有且只有两个不等的实数根?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
参考答案:
【答案】(1)![]() ;(2)详见解析
;(2)详见解析
【解析】
试题分析:(1)根据二次函数小于![]() 的解集,设出解析式,利用单调性求得最大值,解出待定系数.(2)将方程等价转化
的解集,设出解析式,利用单调性求得最大值,解出待定系数.(2)将方程等价转化![]() ,利用
,利用![]() 的导数判断其单调性,利用单调性判断
的导数判断其单调性,利用单调性判断![]() 的根的情况.
的根的情况.
试题解析:解:(1)∵![]() 是二次函数,且
是二次函数,且![]() 的解集是
的解集是![]() ,
,
∴可设![]() ,∴
,∴![]() 在区间
在区间![]() 上的最大值是
上的最大值是![]() .
.
由已知,得![]() ,∴
,∴![]() ,∴
,∴![]()
(2)方程![]() 等价于方程
等价于方程![]() ,
,
设![]() ,则
,则![]() 当
当![]() 时,
时,![]() 是减函数;
是减函数;
当![]() 时,
时,![]() 是增函数.
是增函数.
∵![]()
∴方程![]() 在区间
在区间![]() 内分别有唯一实数根,而在区间
内分别有唯一实数根,而在区间![]() 内没有实数根,所在存在唯一的自然数
内没有实数根,所在存在唯一的自然数![]() ,使得方程
,使得方程![]() 在区间
在区间![]() 内有且只有两上不等的实数根
内有且只有两上不等的实数根
-
科目: 来源: 题型:
查看答案和解析>>【题目】从某校高三上学期期末数学考试成绩中,随机抽取了
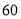 名学生的成绩得到频率分布直方图如下:
名学生的成绩得到频率分布直方图如下: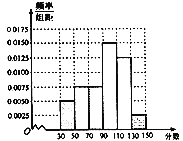
(1)若用分层抽样的方法从分数在
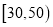 和
和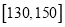 的学生中共抽取
的学生中共抽取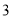 人,该
人,该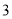 人中成绩在
人中成绩在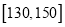 的有几人?
的有几人?(2)在(1)中抽取的
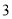 人中,随机抽取
人中,随机抽取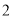 人,求分数在
人,求分数在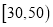 和
和 各
各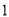 人的概率.
人的概率.(3)根据频率分布直方图,估计该校高三学生本次数学考试的平均分;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车间甲组有10名工人,其中有4名女工人;乙组有10名工人,其中有6名女工人.现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两组共抽取4名工人进行技术考核.
(1)求从甲、乙两组各抽取的人数;
(2)求从甲组抽取的工人中恰有1名女工人的概率;
(3)求抽取的4名工人中恰有2名男工人的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司有30名男职员和20名女职员,公司进行了一次全员参与的职业能力测试,现随机询问了该公司5名男职员和5名女职员在测试中的成绩(满分为30分),可知这5名男职员的测试成绩分别为16,24,18,
22,20,5名女职员的测试成绩分别为18,23,23,18,23,则下列说法一定正确的是( )
A. 这种抽样方法是分层抽样
B. 这种抽样方法是系统抽样
C. 这5名男职员的测试成绩的方差大于这5名女职员的测试成绩的方差
D. 该测试中公司男职员的测试成绩的平均数小于女职员的测试成绩的平均数
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地为制定初中七、八、九年级学生校服的生产计划,有关部门准备对180名初中男生的身高作调查.
(1)为了达到估计该地初中三个年级男生身高分布的目的,你认为采用怎样的调查方案比较合理?
(2)表中的数据是使用了某种调查方法获得的:七、八、九年级180名男生身高:
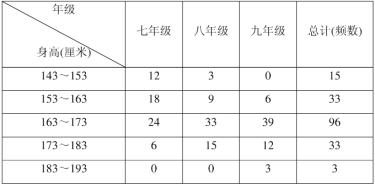
注:表中每组可含最低值,不含最高值.
根据表中的数据,请你给校服生产厂家指定一份生产计划思路.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
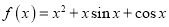 .
.(1)若曲线
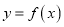 在点
在点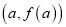 处与直线
处与直线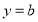 相切,求
相切,求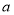 与
与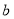 的值;
的值;(2)若曲线
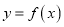 与直线
与直线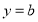 有两个不同交点,求
有两个不同交点,求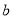 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
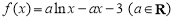 .
.(Ⅰ)当
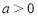 时,求函数
时,求函数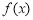 的单调区间;
的单调区间;(Ⅱ)若函数
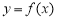 的图象在点
的图象在点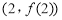 处的切线的倾斜角为
处的切线的倾斜角为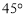 ,且函数
,且函数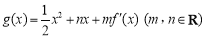 当且仅当在
当且仅当在 处取得极值,其中
处取得极值,其中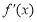 为
为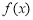 的导函数,求
的导函数,求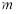 的取值范围;
的取值范围;
相关试题

