【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若函数![]() 的图象在点
的图象在点![]() 处的切线的倾斜角为
处的切线的倾斜角为![]() ,且函数
,且函数![]() 当且仅当在
当且仅当在![]() 处取得极值,其中
处取得极值,其中![]() 为
为![]() 的导函数,求
的导函数,求![]() 的取值范围;
的取值范围;
参考答案:
【答案】(Ⅰ) 单调增区间为![]() 单调减区间为
单调减区间为![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】
试题分析:(Ⅰ)求单调区间,求出函数定义域后,可再求得导数![]() ,在定义域内解不等式
,在定义域内解不等式![]() 得增区间,解不等式
得增区间,解不等式![]() 得减区间;(Ⅱ)本小题中参数较多,首先求出参数值或它们之间的关系,由导数的几何意义可求得
得减区间;(Ⅱ)本小题中参数较多,首先求出参数值或它们之间的关系,由导数的几何意义可求得![]() ,由极值的定义可求得
,由极值的定义可求得![]() 的关系,这样问题中只含有一个参数
的关系,这样问题中只含有一个参数![]() ,由
,由![]() 及极值唯,问题转化为得
及极值唯,问题转化为得![]() 时,
时,![]() 恒成立,由一元二次不等式与二次函数的性质可得
恒成立,由一元二次不等式与二次函数的性质可得![]() 范围.
范围.
试题解析:(Ⅰ)![]() ,
,
当![]() 时,令
时,令![]() 得
得![]() ,令
,令![]() 得
得![]() ,
,
故函数![]() 的单调增区间为
的单调增区间为![]() 单调减区间为
单调减区间为![]() ;
;
(Ⅱ)函数![]() 的图象在点
的图象在点![]() 处的切线的倾斜角为
处的切线的倾斜角为![]() ,
,
则![]() ,即
,即![]() ;
;
所以![]() 所以
所以![]()
因为![]() 在
在![]() 处有极值,故
处有极值,故![]() ,从而可得
,从而可得![]() ,则
,则![]() 又因为
又因为![]() 仅在
仅在![]() 处有极值,
处有极值,
所以![]() 在
在![]() 上恒成立,当
上恒成立,当![]() 时,由
时,由![]() ,即
,即![]() ,使得
,使得![]() ,所以
,所以![]() 不成立,故
不成立,故![]() ,
,
又![]() 且
且![]() 时,
时,![]() 恒成立,
恒成立,
所以![]() ;
;
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
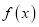 是二次函数,不等式
是二次函数,不等式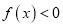 的解集是
的解集是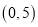 ,且
,且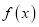 在区间
在区间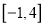 上的最大值是12.
上的最大值是12.(1)求
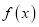 的解析式;
的解析式;(2)是否存在自然数
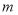 ,使得方程
,使得方程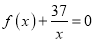 在区间
在区间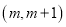 内有且只有两个不等的实数根?若存在,求出
内有且只有两个不等的实数根?若存在,求出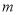 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地为制定初中七、八、九年级学生校服的生产计划,有关部门准备对180名初中男生的身高作调查.
(1)为了达到估计该地初中三个年级男生身高分布的目的,你认为采用怎样的调查方案比较合理?
(2)表中的数据是使用了某种调查方法获得的:七、八、九年级180名男生身高:
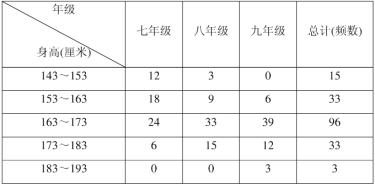
注:表中每组可含最低值,不含最高值.
根据表中的数据,请你给校服生产厂家指定一份生产计划思路.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
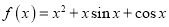 .
.(1)若曲线
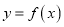 在点
在点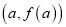 处与直线
处与直线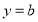 相切,求
相切,求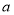 与
与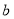 的值;
的值;(2)若曲线
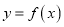 与直线
与直线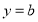 有两个不同交点,求
有两个不同交点,求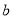 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加了其中一组,在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%.登山组的职工占参加活动总人数的
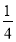 ,且该组中,青年人占50%,中年人占40%,老年人占10%.为了了解各组不同年龄层次的职工对本次活动的满意程度,现用分层抽样方法从参加活动的全体职工中抽取一个容量为200的样本,试确定:
,且该组中,青年人占50%,中年人占40%,老年人占10%.为了了解各组不同年龄层次的职工对本次活动的满意程度,现用分层抽样方法从参加活动的全体职工中抽取一个容量为200的样本,试确定:(1)游泳组中,青年人、中年人、老年人分别所占的比例;
(2)游泳组中,青年人、中年人、老年人分别应抽取的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地区有小学21所,中学14所,大学7所,现采用分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查.
(1)求应从小学、中学、大学中分别抽取的学校数目;
(2)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,
①列出所有可能的抽取结果;
②求抽取的2所学校均为小学的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
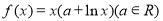 .
.(Ⅰ)当
 时,求
时,求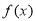 的极值;
的极值;(Ⅱ)若曲线
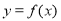 在点
在点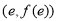 处切线的斜率为3,且
处切线的斜率为3,且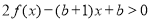 对任意
对任意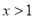 都成立,求整数
都成立,求整数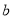 的最大值.
的最大值.
相关试题

