【题目】【2017重庆二诊】已知函数![]() ,
,![]() .
.
(1)分别求函数![]() 与
与![]() 在区间
在区间![]() 上的极值;
上的极值;
(2)求证:对任意![]() ,
, ![]() .
.
参考答案:
【答案】(Ⅰ)![]() 在
在![]() 上有极小值
上有极小值![]() ,无极大值;
,无极大值; ![]() 在
在![]() 上有极大值
上有极大值![]() ,无极小值;(Ⅱ)见解析.
,无极小值;(Ⅱ)见解析.
【解析】(Ⅰ)由题意,利用导数进行求解,首先求出函数极值点,再判断极值点两侧的单调性,从而得出是否为极大值点,还是极小值点,问题即可得解;(Ⅱ)由(Ⅰ)知,可将![]() 分为
分为![]() 和
和![]() 两段进行证明,在区间
两段进行证明,在区间![]() 上可比较两个函数的极小值与极大值即,在区间
上可比较两个函数的极小值与极大值即,在区间![]() 上可考虑将两函数作差构造新函数,再通过判断新函数的单调性和最值,从而问题可得证.
上可考虑将两函数作差构造新函数,再通过判断新函数的单调性和最值,从而问题可得证.
试题解析:(Ⅰ) ![]() ,
, ![]() ,
,
故![]() 在
在![]() 和
和![]() 上递减,在
上递减,在![]() 上递增,
上递增,
![]() 在
在![]() 上有极小值
上有极小值![]() ,无极大值;
,无极大值; ![]() ,
, ![]() ,
,
故![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,
上递减,
![]() 在
在![]() 上有极大值
上有极大值![]() ,无极小值;
,无极小值;
(Ⅱ)由(Ⅰ)知,当![]() 时,
时, ![]() ,
, ![]() ,故
,故![]() ;
;
当![]() 时,
时, ![]() ,令
,令![]() ,则
,则![]() ,
,
故![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,
上递减, ![]() ,
, ![]() ;
;
综上,对任意![]() ,
, ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【2017重庆二诊】已知函数
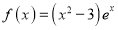 ,设关于
,设关于 的方程
的方程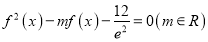 有
有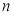 个不同的实数解,则
个不同的实数解,则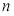 的所有可能的值为( )
的所有可能的值为( )A. 3 B. 1或3 C. 4或6 D. 3或4或6
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an},{bn},Sn为数列{an}的前n项和,向量
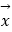 =(1,bn),
=(1,bn),  =(an﹣1,Sn),
=(an﹣1,Sn), 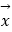 ∥
∥  .
.
(1)若bn=2,求数列{an}通项公式;
(2)若bn= ,a2=0.
,a2=0.
①证明:数列{an}为等差数列;
②设数列{cn}满足cn= ,问是否存在正整数l,m(l<m,且l≠2,m≠2),使得cl、c2、cm成等比数列,若存在,求出l、m的值;若不存在,请说明理由.
,问是否存在正整数l,m(l<m,且l≠2,m≠2),使得cl、c2、cm成等比数列,若存在,求出l、m的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆mx2+ny2=1与直线x+y﹣1=0相交于A,B两点,过AB中点M与坐标原点的直线的斜率为
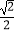 ,则
,则  的值为( )
的值为( )
A.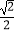
B.
C.1
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}是有穷数列,且a1∈R,公差d=2,记{an}的所有项之和为S,若a12+S≤96,则数列{an}至多有项.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A={(x,y)|(x﹣4)2+y2=1},B={(x,y)|(x﹣t)2+(y﹣at+2)2=1},如果命题“t∈R,A∩B≠”是真命题,则实数a的取值范围是( )
A.[1,4]
B.[0, ]
]
C.[0, ]
]
D.(﹣∞,0]∪( ,+∞]
,+∞] -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形
 中,
中,  ,矩形
,矩形 所在的平面与平面
所在的平面与平面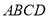 垂直,且
垂直,且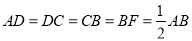 .
.(Ⅰ)求证:平面
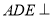 平面
平面 ;
;(Ⅱ)若
 为线段
为线段 上一点,平面
上一点,平面 与平面
与平面 所成的锐二面角为
所成的锐二面角为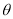 ,求
,求 的最小值.
的最小值.
相关试题

