【题目】如图,梯形![]() 中,
中, ![]() ,矩形
,矩形![]() 所在的平面与平面
所在的平面与平面![]() 垂直,且
垂直,且![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 为线段
为线段![]() 上一点,平面
上一点,平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() ,求
,求![]() 的最小值.
的最小值.

参考答案:
【答案】(1)见解析(2)![]()
【解析】试题分析:(1) 取![]() 中点
中点![]() ,由题意可知四边形BCDM,ADCM均菱形,所以
,由题意可知四边形BCDM,ADCM均菱形,所以![]() ,即AD垂直于再垂直平面的交线,所以
,即AD垂直于再垂直平面的交线,所以![]() 平面BFED,可证平面
平面BFED,可证平面![]() 平面
平面![]() 。(2)以DA,DB,DE分别为x,y,z轴建立空间直角坐标系,
。(2)以DA,DB,DE分别为x,y,z轴建立空间直角坐标系, ![]() ,用夹量建立函数关系
,用夹量建立函数关系 所以
所以![]()
试题解析:(Ⅰ)取![]() 中点
中点![]() ,连接
,连接![]() ,因为AB//CD,
,因为AB//CD, ![]()
所以四边形![]() 为菱形
为菱形![]() ,
, ![]() 所以,
所以, ![]()
因为平面BFED⊥平面ABCD, 平面BFED![]() 平面ABCD
平面ABCD ![]() ,
,
![]() 平面
平面![]() ,所以
,所以![]() 平面BFED.
平面BFED.
又![]() 平面ADE, ∴平面
平面ADE, ∴平面![]() 平面
平面![]() ;
;
(Ⅱ)因为四边形BFED为矩形,所以ED⊥DB,
如图建立空间直角坐标系D-xyz.

设AD=1,则![]()
![]() ,设
,设![]() 是平面PAB的
是平面PAB的
法向量,则
 取
取![]()
又平面![]() 的一个法向量为
的一个法向量为![]()
 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【2017重庆二诊】已知函数
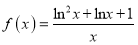 ,
,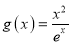 .
.(1)分别求函数
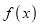 与
与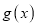 在区间
在区间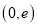 上的极值;
上的极值;(2)求证:对任意
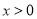 ,
, 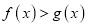 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}是有穷数列,且a1∈R,公差d=2,记{an}的所有项之和为S,若a12+S≤96,则数列{an}至多有项.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A={(x,y)|(x﹣4)2+y2=1},B={(x,y)|(x﹣t)2+(y﹣at+2)2=1},如果命题“t∈R,A∩B≠”是真命题,则实数a的取值范围是( )
A.[1,4]
B.[0, ]
]
C.[0, ]
]
D.(﹣∞,0]∪( ,+∞]
,+∞] -
科目: 来源: 题型:
查看答案和解析>>【题目】为备战
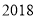 年瑞典乒乓球世界锦标赛,乒乓球队举行公开选拨赛,甲、乙、丙三名选手入围最终单打比赛名单.现甲、乙、丙三人进行队内单打对抗比赛,每两人比赛一场,共赛三场,每场比赛胜者得
年瑞典乒乓球世界锦标赛,乒乓球队举行公开选拨赛,甲、乙、丙三名选手入围最终单打比赛名单.现甲、乙、丙三人进行队内单打对抗比赛,每两人比赛一场,共赛三场,每场比赛胜者得 分,负者得
分,负者得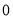 分,在每一场比赛中,甲胜乙的概率为
分,在每一场比赛中,甲胜乙的概率为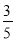 ,丙胜甲的概率为
,丙胜甲的概率为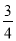 ,乙胜丙的概率为
,乙胜丙的概率为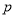 ,且各场比赛结果互不影响.若甲获第一名且乙获第三名的概率为
,且各场比赛结果互不影响.若甲获第一名且乙获第三名的概率为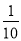 .
.(Ⅰ)求
 的值;
的值;(Ⅱ)设在该次对抗比赛中,丙得分为
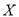 ,求
,求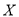 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
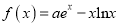 ,其中
,其中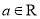 ,
, 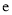 是自然对数的底数.
是自然对数的底数.(Ⅰ)若
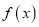 是
是 上的增函数,求
上的增函数,求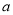 的取值范围;
的取值范围;(Ⅱ)若
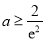 ,证明:
,证明: 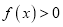 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知点A(2,4),直线l:x﹣2y+1=0.
(1)求过点A且平行于l的直线的方程;
(2)若点M在直线l上,且AM⊥l,求点M的坐标.
相关试题

