【题目】已知函数f(x)是奇函数,当x>0时,f(x)=ax(x>0且a≠1),且f(log ![]() 4)=﹣3,则a的值为( )
4)=﹣3,则a的值为( )
A.![]()
B.3
C.9
D.![]()
参考答案:
【答案】A
【解析】解:∵奇函数f(x)满足f(log ![]() 4)=﹣3,log
4)=﹣3,log ![]() 4=﹣2<0,
4=﹣2<0,
∴f(2)=3
又∵当x>0时,f(x)=ax(x>0且a≠1),2>0
∴f(2)=a2=3,解之得a= ![]() (舍负)
(舍负)
故选A
【考点精析】解答此题的关键在于理解函数奇偶性的性质的相关知识,掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
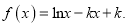
(Ⅰ)若
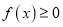 有唯一解,求实数
有唯一解,求实数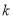 的值;
的值;(Ⅱ)证明:当
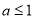 时,
时, 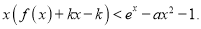
(附:
 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知(
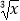 ﹣
﹣ 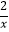 )n的展开式中,第三项的系数为144.
)n的展开式中,第三项的系数为144.
(1)求该展开式中所有偶数项的二项式系数之和;
(2)求该展开式的所有有理项. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=
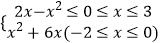 的值域是( )
的值域是( )
A.R
B.[﹣8,1]
C.[﹣9,+∞)
D.[﹣9,1] -
科目: 来源: 题型:
查看答案和解析>>【题目】设a>1,函数f(x)=logax在区间[a,2a]上的最大值与最小值之差为
 ,则a= .
,则a= . -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场举行抽奖活动,规则如下:甲箱子里装有3个白球和2个黑球,乙箱子里装有1个白球和3个黑球,这些球除颜色外完全相同;每次抽奖都从这两个箱子里各随机地摸出2个球,若摸出的白球个数不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(1)在一次游戏中,求获奖的概率;
(2)在三次游戏中,记获奖次数为随机变量X,求X的分布列及期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x)同时满足①对于定义域上的任意x,恒有f(x)+f(﹣x)=0;②对于定义域上的任意x1、x2 , 当x1≠x2时,恒有
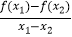 <0,则称函数f(x)为“理想函数”.给出下列三个函数中:(1)f(x)=
<0,则称函数f(x)为“理想函数”.给出下列三个函数中:(1)f(x)= 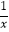 ;(2)f(x)=x+1;(3)f(x)=
;(2)f(x)=x+1;(3)f(x)= 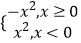 ,能被称为“理想函数”的有(填相应的序号).
,能被称为“理想函数”的有(填相应的序号).
相关试题

