【题目】已知函数![]() 是定义域为
是定义域为![]() 的奇函数.
的奇函数.
(1)求实数![]() 的值并判断函数
的值并判断函数![]() 的单调性;
的单调性;
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)见解析(2)![]() .
.
【解析】分析:(1)由奇函数可得![]() ,解得
,解得![]() ,经检验,当
,经检验,当![]() 时,函数
时,函数![]() 为奇函数;设
为奇函数;设![]() 且
且![]() ,利用指数函数的性质可证明
,利用指数函数的性质可证明![]() ,从而可得结果;(2)结合函数的单调性与奇偶性可得,当
,从而可得结果;(2)结合函数的单调性与奇偶性可得,当![]() 时,不等式
时,不等式![]() 恒成立,等价于
恒成立,等价于![]() 对
对![]() 恒成立,换元后,利用二次函数的性质列不等式组求解即可.
恒成立,换元后,利用二次函数的性质列不等式组求解即可.
详解:(1)解法一:∵函数是定义域为![]() 的奇函数,
的奇函数,
∴![]() ,解得
,解得![]() .
.
经检验,当![]() 时,函数
时,函数![]() 为奇函数,即所求实数
为奇函数,即所求实数![]() 的值为
的值为![]() .
.
∵![]()
![]() ,
,
![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 是
是![]() 上的减函数.
上的减函数.
解法二:∵函数是定义域为![]() 的奇函数,
的奇函数,
∴![]() ,解得
,解得![]() .
.
经检验,当![]() 时,函数
时,函数![]() 为奇函数,即所求实数
为奇函数,即所求实数![]() 的值为
的值为![]() .
.
设![]() 且
且![]() ,
,
则![]()
![]()
![]() ,
,
∵![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
所以![]() 是
是![]() 上的减函数.
上的减函数.
(2)由![]() ,可得
,可得![]() .
.
∵![]() 是
是![]() 上的奇函数,∴
上的奇函数,∴![]() ,
,
又![]() 是
是![]() 上的减函数,
上的减函数,
所以![]() 对
对![]() 恒成立,
恒成立,
令![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
∴![]() 对
对![]() 恒成立,
恒成立,
令![]() ,
,![]() ,
,
∴![]() ,解得
,解得![]() ,
,
所以实数![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着网络营销和电子商务的兴起,人们的购物方式更具多样化,某调查机构随机抽取10名购物者进行采访,5名男性购物者中有3名倾向于选择网购,2名倾向于选择实体店,5名女性购物者中有2名倾向于选择网购,3名倾向于选择实体店.
(1)若从10名购物者中随机抽取2名,其中男、女各一名,求至少1名倾向于选择实体店的概率;
(2)若从这10名购物者中随机抽取3名,设X表示抽到倾向于选择网购的男性购物者的人数,求X的分布列和数学期望.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了比较两种治疗失眠症的药(分别称为
 药,
药,  药)的疗效,随机地选取18位患者服用
药)的疗效,随机地选取18位患者服用 药,18位患者服用
药,18位患者服用 药,这36位患者服用一段时间后,记录他们日平均增加的睡眠时间(单位:
药,这36位患者服用一段时间后,记录他们日平均增加的睡眠时间(单位: ),试验的观测结果如下:
),试验的观测结果如下:服用
 药的18位患者日平均增加的睡眠时间:
药的18位患者日平均增加的睡眠时间:0.6 1.2 2.7 1.5 2.8 1.8 2.2 2.3 3.2 2.5 2.6 1.2 2.7 1.5 2.9 3.0 3.1 2.3
服用
 药的18位患者日平均增加的睡眠时间:
药的18位患者日平均增加的睡眠时间:3.2 1.7 1.9 0.8 0.9 2.4 1.2 2.6 1.3 1.6 0.5 1.8 0.6 2.1 1.1 2.5 1.2 2.7
(1)分别计算两组数据的平均数(小数点后保留两位小数),从计算结果看哪种药疗效更好?
(2)根据两组数据完成下面茎叶图,从茎叶图看,哪种药的疗效更好?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】随着经济的发展,某地最近几年某商品的需求量逐年上升.下表为部分统计数据:
年份






需求量
 (万件)
(万件)




为了研究计算的方便,工作人员将上表的数据进行了处理,令
 ,
, .
.(1)填写下列表格并求出
 关于
关于 的线性回归方程:
的线性回归方程:时间代号

 (万件)
(万件)(2)根据所求的线性回归方程,预测到
 年年底,某地对该商品的需求量是多少?
年年底,某地对该商品的需求量是多少?(附:线性回归方程
 ,其中
,其中 ,
, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】驻马店市政府委托市电视台进行“创建森林城市”知识问答活动,市电视台随机对该市15~65岁的人群抽取了
 人,绘制出如图1所示的频率分布直方图,回答问题的统计结果如表2所示.
人,绘制出如图1所示的频率分布直方图,回答问题的统计结果如表2所示.
(1)分别求出
 的值;
的值;(2)从第二、三、四、五组回答正确的人中用分层抽样的方法抽取7人,则从第二、三、四、五组每组回答正确的人中应各抽取多少人?
(3)在(2)的条件下,电视台决定在所抽取的7人中随机选2人颁发幸运奖,求所抽取的人中第二组至少有1人获得幸运奖的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知不等式
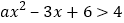 的解集为
的解集为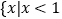 或
或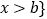 .
.(1)求
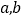 ;(2)解关于
;(2)解关于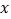 的不等式
的不等式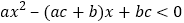
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在(0,+∞)上的连续函数y=f(x)满足:xf′(x)﹣f(x)=xex且f(1)=﹣3,f(2)=0.则函数y=f(x)( )
A.有极小值,无极大值
B.有极大值,无极小值
C.既有极小值又有极大值
D.既无极小值又无极大值
相关试题

