【题目】空气质量指数AQI是一种反映和评价空气质量的方法,AQI指数与空气质量对应如表所示:
AQI | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | 300以上 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
如图是某城市2018年12月全月的AQI指数变化统计图:

根据统计图判断,下列结论正确的是( )
A. 整体上看,这个月的空气质量越来越差
B. 整体上看,前半月的空气质量好于后半个月的空气质量
C. 从AQI数据看,前半月的方差大于后半月的方差
D. 从AQI数据看,前半月的平均值小于后半月的平均值
参考答案:
【答案】C
【解析】
根据题意可得,AQI指数越高,空气质量越差;数据波动越大,方差就越大,由此逐项判断,即可得出结果.
从整体上看,这个月AQI数据越来越低,故空气质量越来越好;故A,B不正确;
从AQI数据来看,前半个月数据波动较大,后半个月数据波动小,比较稳定,因此前半个月的方差大于后半个月的方差,所以C正确;
从AQI数据来看,前半个月数据大于后半个月数据,因此前半个月平均值大于后半个月平均值,故D不正确.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业有甲、乙两套设备生产同一种产品,为了检测两套设备的生产质量情况,随机从两套设备生产的大量产品中各随机抽取了100件产品作为样本来检测一项质量指标值,若产品的该项质量指标值落在
 内,则为合格品,否则为不合格品.表1是甲套设备的样本的频数分布表,图是乙套设备的样本的频率分布直方图.
内,则为合格品,否则为不合格品.表1是甲套设备的样本的频数分布表,图是乙套设备的样本的频率分布直方图.
表甲套设备的样本的频数分布表
质量指标值
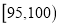





频数
2
10
36
38
12
2
(1)将频率视为概率.若乙套设备生产了10000件产品,则其中的合格品约有多少件?
(2)填写下面的2×2列联表,并判断能否在犯错误的概率不超过0.01的前提下,认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关.
甲套设备
乙套设备
合计
合格品
不合格品
合计
附表及公式:
 ,其中
,其中 ;
;
0.10
0.05
0.025
0.010
0.005
0.001

2.706
3.841
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知三棱柱
 ,平面
,平面 平面
平面 ,
, ,
, 分别是
分别是 的中点.
的中点.
(1)证明:
 ;
;(2)求直线
 与平面
与平面 所成角的余弦值.
所成角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
 的一个焦点与抛物线y2=-4x的焦点相同,且椭圆C上一点与椭圆C的左,右焦点F1,F2构成的三角形的周长为
的一个焦点与抛物线y2=-4x的焦点相同,且椭圆C上一点与椭圆C的左,右焦点F1,F2构成的三角形的周长为 .
.(1)求椭圆C的方程;
(2)若直线l:y=kx+m(k,m∈R)与椭圆C交于A,B两点,O为坐标原点,△AOB的重心G满足:
 ,求实数m的取值范围.
,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某酱油厂对新品种酱油进行了定价,在各超市得到售价与销售量的数据如下表:
单价
 (元)
(元)5
5.2
5.4
5.6
5.8
6
销量
 (瓶)
(瓶)9.0
8.4
8.3
8.0
7.5
6.8
(1)求售价与销售量的回归直线方程;(
 ,
, )
)(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/瓶,为使工厂获得最大利润(利润=销售收入
 成本),该产品的单价应定为多少元?
成本),该产品的单价应定为多少元?相关公式:
 ,
,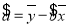 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】【选修4-4:坐标系与参数方程】
在平面直角坐标系
 中,曲线
中,曲线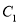 的参数方程为:
的参数方程为:  (
( 为参数,
为参数,  ),将曲线
),将曲线 经过伸缩变换:
经过伸缩变换:  得到曲线
得到曲线 .
.(1)以原点为极点,
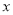 轴的正半轴为极轴建立坐标系,求
轴的正半轴为极轴建立坐标系,求 的极坐标方程;
的极坐标方程;(2)若直线
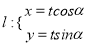 (
( 为参数)与
为参数)与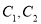 相交于
相交于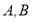 两点,且
两点,且 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
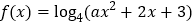
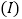 若
若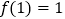 ,求
,求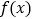 的单调区间;
的单调区间;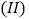 是否存在实数a,使
是否存在实数a,使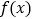 的最小值为0?若存在,求出a的值;若不存在,说明理由.
的最小值为0?若存在,求出a的值;若不存在,说明理由.
相关试题

