【题目】如图,已知三棱柱![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.

(1)证明:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由题意首先证得线面垂直,然后利用线面垂直的定义即可证得线线垂直;
(2)建立空间直角坐标系,分别求得直线的方向向量和平面的法向量,然后结合线面角的正弦值和同角三角函数基本关系可得线面角的余弦值.
(1)如图所示,连结![]() ,
,
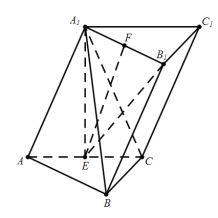
等边![]() 中,
中,![]() ,则
,则![]() ,
,
平面ABC⊥平面![]() ,且平面ABC∩平面
,且平面ABC∩平面![]() ,
,
由面面垂直的性质定理可得:![]() 平面
平面![]() ,故
,故![]() ,
,
由三棱柱的性质可知![]() ,而
,而![]() ,故
,故![]() ,且
,且![]() ,
,
由线面垂直的判定定理可得:![]() 平面
平面![]() ,
,
结合![]() 平面
平面![]() ,故
,故![]() .
.
(2)在底面ABC内作EH⊥AC,以点E为坐标原点,EH,EC,![]() 方向分别为x,y,z轴正方向建立空间直角坐标系
方向分别为x,y,z轴正方向建立空间直角坐标系![]() .
.
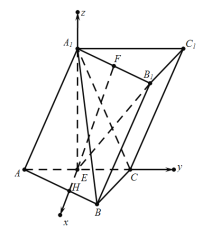
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
据此可得: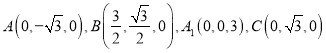 ,
,
由![]() 可得点
可得点![]() 的坐标为
的坐标为![]() ,
,
利用中点坐标公式可得:![]() ,由于
,由于![]() ,
,
故直线EF的方向向量为:![]()
设平面![]() 的法向量为
的法向量为![]() ,则:
,则:
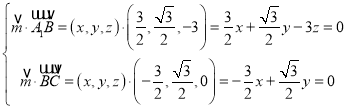 ,
,
据此可得平面![]() 的一个法向量为
的一个法向量为![]() ,
,![]()
此时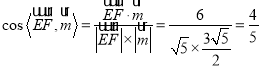 ,
,
设直线EF与平面![]() 所成角为
所成角为![]() ,则
,则![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义在
 上的函数
上的函数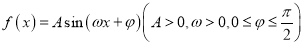 ,若已知其在
,若已知其在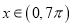 内只取到一个最大值和一个最小值,且当
内只取到一个最大值和一个最小值,且当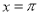 时函数取得最大值为
时函数取得最大值为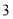 ;当
;当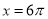 ,函数取得最小值为
,函数取得最小值为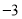 .
.(1)求出此函数的解析式;
(2)若将函数
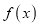 的图像保持横坐标不变纵坐标变为原来的
的图像保持横坐标不变纵坐标变为原来的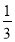 得到函数
得到函数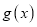 ,再将函数
,再将函数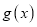 的图像向左平移
的图像向左平移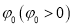 个单位得到函数
个单位得到函数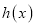 ,已知函数
,已知函数 的最大值为
的最大值为 ,求满足条件的
,求满足条件的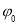 的最小值;
的最小值;(3)是否存在实数
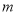 ,满足不等式
,满足不等式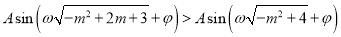 ?若存在,求出
?若存在,求出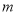 的范围(或值),若不存在,请说明理由.
的范围(或值),若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某测试团队为了研究“饮酒”对“驾车安全”的影响,随机选取
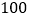 名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试.测试的方案:电脑模拟驾驶,以某速度匀速行驶,记录下驾驶员的“停车距离”(驾驶员从看到意外情况到车子完全停下所需要的距离).无酒状态与酒后状态下的试验数据分别列于表1和表2.
名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试.测试的方案:电脑模拟驾驶,以某速度匀速行驶,记录下驾驶员的“停车距离”(驾驶员从看到意外情况到车子完全停下所需要的距离).无酒状态与酒后状态下的试验数据分别列于表1和表2.表1
停车距离
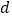 (米)
(米)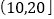

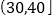
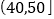

频数
24
42
24
9
1
表2
平均每毫升血液酒精含量
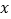 毫克
毫克10
30
50
70
90
平均停车距离
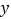 米
米30
50
60
70
90
回答以下问题.
(1)由表1估计驾驶员无酒状态下停车距离的平均数;
(2)根据最小二乘法,由表2的数据计算
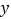 关于
关于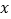 的回归方程
的回归方程 ;
;(3)该测试团队认为:驾驶员酒后驾车的平均“停车距离”
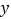 大于(1)中无酒状态下的停车距离平均数的
大于(1)中无酒状态下的停车距离平均数的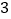 倍,则认定驾驶员是“醉驾”.请根据(2)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?(精确到个位)
倍,则认定驾驶员是“醉驾”.请根据(2)中的回归方程,预测当每毫升血液酒精含量大于多少毫克时为“醉驾”?(精确到个位)(附:对于一组数据
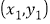 ,
,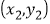 ,…,
,…,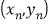 ,其回归直线
,其回归直线 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为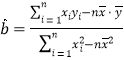 ,
,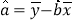 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列四种说法:
(1)函数
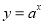
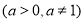 与函数
与函数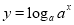
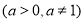 的定义域相同;
的定义域相同;(2)函数
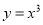 与
与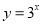 的值域相同;
的值域相同;(3)若函数
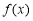 式定义在R上的偶函数且在
式定义在R上的偶函数且在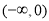 为减函数对于锐角
为减函数对于锐角 则
则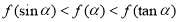 ;
;(4)若函数
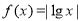 且
且
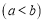 ,则
,则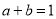 ;
;其中正确说法的序号是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知函数
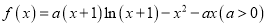 是减函数,则实数
是减函数,则实数 ( )
( )A.2B.1C.
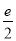 D.
D.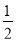
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
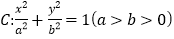 的两个焦点与短轴的一个顶点构成底边为
的两个焦点与短轴的一个顶点构成底边为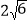 ,顶角为
,顶角为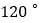 的等腰三角形.
的等腰三角形.(1)求椭圆
 的方程;
的方程;(2)设
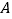 、
、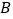 、
、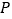 是椭圆上三动点,且
是椭圆上三动点,且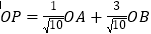 ,线段
,线段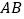 的中点为
的中点为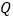 ,
, ,求
,求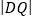 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(管道构成Rt△FHE,H是直角项点)来处理污水.管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,AD=
 米,记∠BHE=
米,记∠BHE= .
.
(1)试将污水净化管道的长度L表示为
 的函数,并写出定义域;
的函数,并写出定义域;(2)当
 取何值时,污水净化效果最好?并求出此时管道的长度L.
取何值时,污水净化效果最好?并求出此时管道的长度L.
相关试题

