【题目】已知椭圆C: ![]() 的一个焦点与抛物线y2=-4x的焦点相同,且椭圆C上一点与椭圆C的左,右焦点F1,F2构成的三角形的周长为
的一个焦点与抛物线y2=-4x的焦点相同,且椭圆C上一点与椭圆C的左,右焦点F1,F2构成的三角形的周长为![]() .
.
(1)求椭圆C的方程;
(2)若直线l:y=kx+m(k,m∈R)与椭圆C交于A,B两点,O为坐标原点,△AOB的重心G满足: ![]() ,求实数m的取值范围.
,求实数m的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)利用与抛物线有公共焦点、椭圆的定义及几何要素间的等量关系进行求解;(2)联立直线和椭圆的方程,得到关于![]() 的一元二次方程,利用根与系数的关系、三角形的重心性质和平面向量的数量积运算进行求解.
的一元二次方程,利用根与系数的关系、三角形的重心性质和平面向量的数量积运算进行求解.
试题解析:(1)依题意得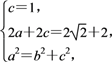
即![]()
所以椭圆C的方程为![]() +y2=1.
+y2=1.
(2)设A(x1,y1),B(x2,y2),
联立得方程组![]()
消去y并整理得(1+2k2)x2+4kmx+2m2-2=0,
则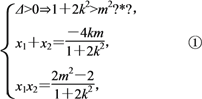
设△AOB的重心为G(x,y),
由![]() ·
·![]() =-
=-![]() ,
,
可得x2+y2=![]() .②
.②
由重心公式可得G(![]() ,
,![]() ),
),
代入②式,整理可得(x1+x2)2+(y1+y2)2=4(x1+x2)2+[k(x1+x2)+2m]2=4,③
将①式代入③式并整理,
得m2=![]() ,
,
代入(*)得k≠0,
则m2=![]() =1+
=1+![]() =1+
=1+![]() .
.
∵k≠0,∴t=![]() >0,∴t2+4t>0,
>0,∴t2+4t>0,
∴m2>1,∴m∈(-∞,-1)∪(1,+∞).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某运输公司接受了向一地区每天至少运送180 t物资的任务,该公司有8辆载重为6 t的A型卡车和4辆载重为10 t的B型卡车,有10名驾驶员,每辆卡车每天往返的次数为A型卡车4次,B型卡车3次,每辆卡车每天往返的费用为A型卡车320元,B型卡车504元,则公司如何调配车辆,才能使公司所花的费用最低,最低费用为________元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆E:
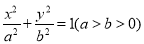 ,其焦点为F1,F2,离心率为
,其焦点为F1,F2,离心率为 ,直线l:x+2y-2=0与x轴,y轴分别交于点A,B,
,直线l:x+2y-2=0与x轴,y轴分别交于点A,B,(1)若点A是椭圆E的一个顶点,求椭圆的方程;
(2)若线段AB上存在点P满足|PF1|+|PF2|=2a,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(-2,0),B(2,0),曲线C上的动点P满足
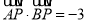 .
.(1)求曲线C的方程;
(2)若过定点M(0,-2)的直线l与曲线C有公共点,求直线l的斜率k的取值范围;
(3)若动点Q(x,y)在曲线C上,求
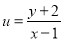 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某人为研究中学生的性别与每周课外阅读量这两个变量的关系,随机抽查了100名中学生,得到频率分布直方图(如图所示),其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12].

(Ⅰ)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生周课外阅读时间的平均数.
(Ⅱ)在样本数据中,有20位女生的每周课外阅读时间超过4小时,15位男生的每周课外阅读时间没有超过4小时.请画出每周课外阅读时间与性别列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“该校学生的每周课外阅读时间与性别有关”.
P(K2≥k0)
0.10
0.05
0.010
0.005
k0
2.706
3.841
6.635
7.879
附:
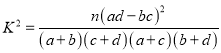
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB是圆O的直径,C,D是圆上不同两点,且CD∩AB=H,AC=AD,PA⊥圆O所在平面.
(Ⅰ)求证:PB⊥CD;
(Ⅱ)若PB=
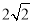 ,∠PBA=
,∠PBA=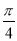 ,∠CAD=
,∠CAD=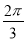 ,求H到平面PBD的距离.
,求H到平面PBD的距离.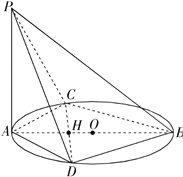
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆G:
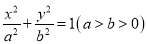 的离心率为
的离心率为 ,过椭圆G右焦点F的直线m:x=1与椭圆G交于点M(点M在第一象限).
,过椭圆G右焦点F的直线m:x=1与椭圆G交于点M(点M在第一象限).(Ⅰ)求椭圆G的方程;
(Ⅱ)已知A为椭圆G的左顶点,平行于AM的直线l与椭圆G相交于B,C两点,请判断直线MB,MC是否关于直线m对称,并说明理由.
相关试题

