【题目】已知函数![]() .
.
(1)当![]() ,
, ![]() 取一切非负实数时,若
取一切非负实数时,若![]() ,求
,求![]() 的范围;
的范围;
(2)若函数![]() 存在极大值
存在极大值![]() ,求
,求![]() 的最小值.
的最小值.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)当![]() 时,
时, ![]() ,原题分离参数得
,原题分离参数得![]() 恒成立,右边求导求出其最大值即可;(2)对其求导
恒成立,右边求导求出其最大值即可;(2)对其求导![]() ,当
,当![]() 时,
时, ![]() 在
在![]() 上为单增函数,无极大值;当
上为单增函数,无极大值;当![]() 时,
时, ![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数,其中
上为减函数,其中![]() 满足
满足![]() ,故可得极大值
,故可得极大值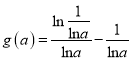 ,令
,令![]() ,得
,得![]() ,对其求导可得其最小值.
,对其求导可得其最小值.
试题解析:(1)当![]() 时,
时, ![]() ,
, ![]() 恒成立等价于
恒成立等价于![]() 恒成立,令
恒成立,令![]() ,
, ![]() ,
, ![]() ,当
,当![]() 时,
时, ![]() 恒成立,即
恒成立,即![]() 在
在![]() 内单调递减,故
内单调递减,故![]() ,可得
,可得![]() 在
在![]() 内单调递减,故
内单调递减,故![]() .
.
(2)![]() ,
,
①当![]() 时,
时, ![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 上为单增函数,无极大值;
上为单增函数,无极大值;
②当![]() 时,设方程
时,设方程![]() 的根为
的根为![]() ,则有
,则有![]() ,即
,即 ,所以
,所以![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数,所以
上为减函数,所以![]() 的极大值为
的极大值为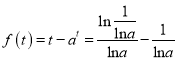 ,即
,即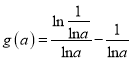 ,因为
,因为![]() ,所以
,所以![]() ,令
,令![]() 则
则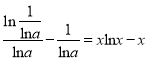 ,
,
设![]() ,则
,则![]() ,令
,令![]() ,得
,得![]() ,所以
,所以![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数,所以
上为增函数,所以![]() 得最小值为
得最小值为![]() ,即
,即![]() 的最小值为-1,此时
的最小值为-1,此时![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2x+2﹣x ,
(1)判断函数的奇偶性;
(2)用函数单调性定义证明:f(x)在(0,+∞)上为单调增函数;
(3)若f(x)=52﹣x+3,求x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和Sn=3n+m(m为常数,n∈N+)
(1)求a1 , a2 , a3;
(2)若数列{an}为等比数列,求常数m的值及an;
(3)对于(2)中的an , 记f(n)=λa2n+1﹣4λan+1﹣7,若f(n)<0对任意的正整数n恒成立,求实数λ的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
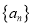 为公差不为
为公差不为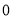 的等差数列,
的等差数列, 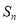 为前
为前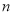 项和,
项和, 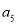 和
和 的等差中项为
的等差中项为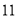 ,且
,且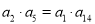 .令
.令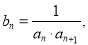 数列
数列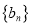 的前
的前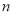 项和为
项和为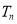 .
.(1)求
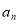 及
及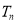 ;
;(2)是否存在正整数
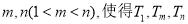 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的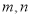 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市共有初中学生270000人,其中初一年级,初二年级,初三年级学生人数分别为99000,90000,81000,为了解该市学生参加“开放性科学实验活动”的意向,现采用分层抽样的方法从中抽取一个容量为3000的样本,那么应该抽取初三年级的人数为( )
A.800
B.900
C.1000
D.1100 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,设抛物线
 的准线
的准线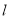 与
与 轴交于椭圆
轴交于椭圆 的右焦点
的右焦点 为
为 的左焦点.椭圆的离心率为
的左焦点.椭圆的离心率为 ,抛物线
,抛物线 与椭圆
与椭圆 交于
交于 轴上方一点
轴上方一点 ,连接
,连接 并延长其交
并延长其交 于点
于点 ,
,  为
为 上一动点,且在
上一动点,且在 之间移动.
之间移动.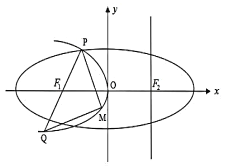
(1)当
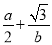 取最小值时,求
取最小值时,求 和
和 的方程;
的方程;(2)若
 的边长恰好是三个连续的自然数,当
的边长恰好是三个连续的自然数,当 面积取最大值时,求面积最大值以及此时直线
面积取最大值时,求面积最大值以及此时直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】某出租车公司响应国家节能减排的号召,已陆续购买了140辆纯电动汽车作为运营车辆,目前我国主流纯电动汽车按续航里程数
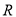 .(单位:公里)分为3类,即
.(单位:公里)分为3类,即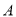 类:
类: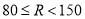 ,
,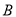 类:
类: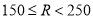 ,
, 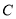 类:
类: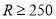 ,该公司对这140辆车的行驶总里程进行统计,结果如下表:
,该公司对这140辆车的行驶总里程进行统计,结果如下表:类型
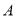 类
类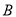 类
类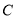 类
类已行驶总里程不超过10万公里的车辆数
10
40
30
已行驶总里程超过10万公里的车辆数
20
20
20
(1)从这140辆汽车中任取一辆,求该车行驶总里程超过10万公里的概率;
(2)公司为了了解这些车的工作状况,决定抽取了14辆车进行车况分析,按表中描述的六种情况进行分层抽样,设从
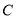 类车中抽取了
类车中抽取了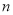 辆车.
辆车.①求
 的值;
的值;②如果从这
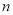 辆车中随机选取两辆车,求恰有一辆车行驶总里程超过10万公里的概率.
辆车中随机选取两辆车,求恰有一辆车行驶总里程超过10万公里的概率.
相关试题

