【题目】求满足下列条件的直线的方程:
(1)直线![]() 经过点
经过点![]() ,并且它的倾斜角等于直线
,并且它的倾斜角等于直线![]() 的倾斜角的2倍,求直线
的倾斜角的2倍,求直线![]() 的方程;
的方程;
(2)直线![]() 过点
过点![]() ,并且在
,并且在![]() 轴上的截距是
轴上的截距是![]() 轴上截距的
轴上截距的![]() ,求直线
,求直线![]() 的方程.
的方程.
参考答案:
【答案】(1)![]() (2)
(2)![]() 或
或![]() .
.
【解析】分析:(1)设直线![]() 的倾斜角为
的倾斜角为![]() ,则
,则![]() ,可得
,可得
∴直线![]() 的斜率为
的斜率为![]() ,由点斜式可得结果;(2)若直线
,由点斜式可得结果;(2)若直线![]() 在两轴上的截距均为0,由直线
在两轴上的截距均为0,由直线![]() 过点
过点![]() ,可得直线方程为
,可得直线方程为![]() ,若直线
,若直线![]() 在两轴上的截距均不为0,设直线
在两轴上的截距均不为0,设直线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,将点
,将点![]() 代入,截距式方程
代入,截距式方程![]() 可得
可得![]() ,从而可得结果.
,从而可得结果.
详解:(1)设直线![]() 的倾斜角为
的倾斜角为![]() ,则
,则![]()
∴
∴直线![]() 的斜率为
的斜率为![]()
又∵直线![]() 经过点
经过点![]()
∴直线![]() 的方程为:
的方程为:![]() 即
即![]()
(2)若直线![]() 在两轴上的截距均不为0,设直线
在两轴上的截距均不为0,设直线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() (
(![]() ),则直线
),则直线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,可设
,可设![]() :
:![]() (
(![]() ),将点
),将点![]() 代入,得
代入,得![]()
∴直线![]() :
:![]() 即
即![]()
若直线![]() 在两轴上的截距均为0,由直线
在两轴上的截距均为0,由直线![]() 过点
过点![]() ,可得直线方程为
,可得直线方程为![]() .
.
∴直线![]() 的方程是:
的方程是:![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数列{an}的各项均为正数,a1=t,k∈N* , k≥1,p>0,an+an+1+an+2+…+an+k=6pn .
(1)当k=1,p=5时,若数列{an}成等比数列,求t的值;
(2)设数列{an}是一个等比数列,求{an}的公比及t(用p、k的代数式表示);
(3)当k=1,t=1时,设Tn=a1+ +
+  +…+
+…+  +
+  ,参照教材上推导等比数列前n项和公式的推导方法,求证:{
,参照教材上推导等比数列前n项和公式的推导方法,求证:{  Tn﹣
Tn﹣  ﹣6n}是一个常数.
﹣6n}是一个常数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示(单位:cm),四边形ABCD是直角梯形,求图中阴影部分绕AB旋转一周所成几何体的表面积和体积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥
 中,
中, 平面
平面 ,
, 是正三角形,
是正三角形, 与
与 的交点
的交点 恰好是
恰好是 中点,又
中点,又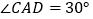 ,
, ,点
,点 在线段
在线段 上,且
上,且 .
.
(
 )求证:
)求证: .
.(
 )求证:
)求证: 平面
平面 .
.(
 )设平面
)设平面 平面
平面 ,试问:直线
,试问:直线 是否与直线
是否与直线 平行,请说明理由.
平行,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.

(1)证明:MN∥平面PAB;
(2)求直线AN与平面PMN所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x||x+1|<1},B={x|(
 )x﹣2≥0},则A∩RB=( )
)x﹣2≥0},则A∩RB=( )
A.(﹣2,﹣1)
B.(﹣2,﹣1]
C.(﹣1,0)
D.[﹣1,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四棱锥P-ABCD,
 底面
底面 ,且底面ABCD是边长为2的正方形,M、N分别为PB、PC的中点.
,且底面ABCD是边长为2的正方形,M、N分别为PB、PC的中点.
(1)证明:MN//平面PAD;
(2)若PA与平面ABCD所成的角为
 ,求四棱锥P-ABCD的体积V.
,求四棱锥P-ABCD的体积V.
相关试题

