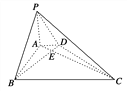
【题目】如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,AC∩BD=E,AD=2,AB=2![]() ,BC=6,求证:平面PBD⊥平面PAC.
,BC=6,求证:平面PBD⊥平面PAC.
参考答案:
【答案】详见解析
【解析】试题分析:先由![]() 平面
平面![]() 可证明
可证明![]() ,由直角三角形的性质可得
,由直角三角形的性质可得![]() ,再由线面垂直的判定定理可得
,再由线面垂直的判定定理可得![]() 平面
平面![]() ,利用面面垂直的判定定理可得结果.
,利用面面垂直的判定定理可得结果.
试题解析:∵PA⊥平面ABCD,
BD平面ABCD,∴BD⊥PA.
又tan∠ABD=![]() =
=![]() . tan∠BAC=
. tan∠BAC=![]() =
=![]() .
.
∴∠ABD=30°,∠BAC=60°,
∴∠AED=90°,即BD⊥AC.
又PA∩AC=A,∴BD⊥平面PAC.
∵BD平面PBD.
所以平面PBD⊥平面PAC.
【方法点晴】本题主要考查线面垂直的判定定理及面面垂直的判定定理,属于难题.解答空间几何体中垂直关系时,一般要根据已知条件把空间中的线线、线面、面面之间垂直关系进行转化,转化时要正确运用有关的定理,找出足够的条件进行推理;要证明面面垂直只需证明线面垂直,证明直线和平面垂直的常用方法有:(1)利用判定定理;(2)利用判定定理的推论![]() ;(3)利用面面平行的性质
;(3)利用面面平行的性质![]() ;(4)利用面面垂直的性质,当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.
;(4)利用面面垂直的性质,当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知函数f(x)的定义域为[0,1],求f(x2+1)的定义域;
(2)已知f(
 )的定义域为[0,3],求f(x)的定义域.
)的定义域为[0,3],求f(x)的定义域. -
科目: 来源: 题型:
查看答案和解析>>【题目】在极坐标系下,已知曲线C1:ρ=cosθ+sinθ和曲线C2:ρsin(θ-
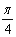 )=
)=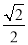 .
.(1)求曲线C1和曲线C2的直角坐标方程;
(2)当θ∈(0,π)时,求曲线C1和曲线C2公共点的一个极坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
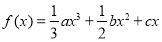 (
(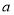 ,
,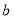 ,
,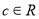 ,
,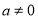 )的图象在点
)的图象在点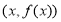 处的切线的斜率为
处的切线的斜率为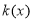 ,且函数
,且函数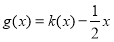 为偶函数.若函数
为偶函数.若函数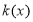 满足下列条件:①
满足下列条件:①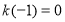 ;②对一切实数
;②对一切实数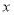 ,不等式
,不等式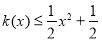 恒成立.
恒成立.(1)求函数
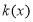 的表达式;
的表达式;(2)设函数
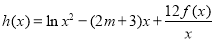 (
(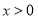 )的两个极值点
)的两个极值点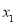 ,
,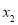 (
(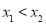 )恰为
)恰为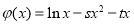 的零点,当
的零点,当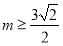 时,求
时,求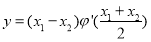 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙C:x2+y2+2x-4y+1=0.
(1)若⊙C的切线在x轴、y轴上截距相等,求切线的方程.
(2)从圆外一点P(x0,y0)向圆引切线PM,M为切点,O为原点,若|PM|=|PO|,求使|PM|最小的P点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.
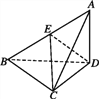
(1)求证:平面ABC⊥平面ACD;
(2)若E为AB中点,求点A到平面CED的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 .
.(1)求f(2)+f
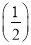 ,f(3)+f
,f(3)+f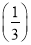 的值;
的值;(2)求证:f(x)+f
 是定值;
是定值;(3)求f(2)+f
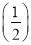 +f(3)+f
+f(3)+f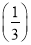 +…+
+…+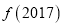 +f
+f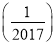 的值.
的值.
相关试题

