【题目】在极坐标系下,已知曲线C1:ρ=cosθ+sinθ和曲线C2:ρsin(θ-![]() )=
)=![]() .
.
(1)求曲线C1和曲线C2的直角坐标方程;
(2)当θ∈(0,π)时,求曲线C1和曲线C2公共点的一个极坐标.
参考答案:
【答案】(1)x2+y2-x-y=0,x-y+1=0;(2)![]() .
.
【解析】试题分析:(1)对![]() 的极坐标方程两边同乘
的极坐标方程两边同乘![]() ,将
,将![]() 的极坐标方程展开,再利用
的极坐标方程展开,再利用![]() 即可得曲线C1和曲线C2的直角坐标方程;(2)曲线C1和曲线C2的直角坐标方程联立,求得曲线
即可得曲线C1和曲线C2的直角坐标方程;(2)曲线C1和曲线C2的直角坐标方程联立,求得曲线![]() 与曲线
与曲线![]() 有公共点的一个直角坐标,再化为极坐标即可.
有公共点的一个直角坐标,再化为极坐标即可.
试题解析:(1)圆O:ρ=cos θ+sin θ,即ρ2=ρcos θ+ρsin θ,
曲线C1的直角坐标方程为:x2+y2=x+y,即x2+y2-x-y=0,
曲线C2:ρsin![]() =
=![]() ,即ρsin θ-ρcos θ=1,
,即ρsin θ-ρcos θ=1,
则曲线C2的直角坐标方程为:y-x=1,即x-y+1=0.
(2)由![]() 得
得![]()
则曲线C1和曲线C2公共点的一个极坐标为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
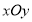 中,直线
中,直线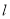 的方程为
的方程为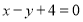 ,曲线
,曲线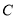 的参数方程为
的参数方程为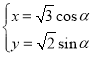 (
(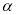 为参数).
为参数).(1)已知在极坐标系(与直角坐标系
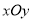 取相同的长度单位,且以原点
取相同的长度单位,且以原点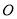 为极点,以
为极点,以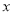 轴正半轴为极轴)中,点
轴正半轴为极轴)中,点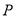 的极坐标为
的极坐标为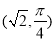 ,判断点
,判断点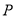 与曲线
与曲线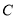 的位置关系;
的位置关系;(2)设点
 是曲线
是曲线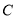 上的一个动点,求它到直线
上的一个动点,求它到直线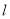 的距离的最小值.
的距离的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业生产某种产品时的能耗y与产品件数x之间的关系式为y=ax+
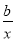 .且当x=2时,y=100;当x=7时,y=35.且此产品生产件数不超过20件.
.且当x=2时,y=100;当x=7时,y=35.且此产品生产件数不超过20件.(1)写出函数y关于x的解析式;
(2)用列表法表示此函数,并画出图象.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知函数f(x)的定义域为[0,1],求f(x2+1)的定义域;
(2)已知f(
 )的定义域为[0,3],求f(x)的定义域.
)的定义域为[0,3],求f(x)的定义域. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
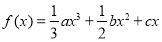 (
(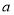 ,
,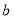 ,
,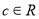 ,
,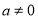 )的图象在点
)的图象在点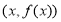 处的切线的斜率为
处的切线的斜率为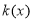 ,且函数
,且函数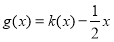 为偶函数.若函数
为偶函数.若函数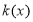 满足下列条件:①
满足下列条件:①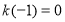 ;②对一切实数
;②对一切实数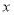 ,不等式
,不等式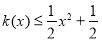 恒成立.
恒成立.(1)求函数
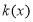 的表达式;
的表达式;(2)设函数
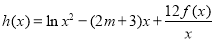 (
(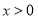 )的两个极值点
)的两个极值点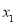 ,
,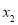 (
(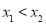 )恰为
)恰为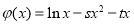 的零点,当
的零点,当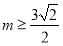 时,求
时,求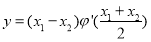 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,AC∩BD=E,AD=2,AB=2
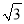 ,BC=6,求证:平面PBD⊥平面PAC.
,BC=6,求证:平面PBD⊥平面PAC. 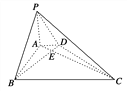
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙C:x2+y2+2x-4y+1=0.
(1)若⊙C的切线在x轴、y轴上截距相等,求切线的方程.
(2)从圆外一点P(x0,y0)向圆引切线PM,M为切点,O为原点,若|PM|=|PO|,求使|PM|最小的P点坐标.
相关试题

