【题目】设数列![]() 满足:
满足:![]()
![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
参考答案:
【答案】(1) ;(2)
;(2)![]()
![]()
【解析】
(1)根据题意,可得a1+2a2+3a3++(n﹣1)an﹣1=2n﹣1,两者相减,可得数列{an}的通项公式;
(2)根据题意,求出bn的通项公式,利用错位相减法求出数列{bn}的前n项和Sn.
(1)∵a1+2a2+3a3+…+nan=2n①,
∴n≥2时,a1+2a2+3a3+…+(n﹣1)an﹣1=2n﹣1②
①﹣②得nan=2n﹣1,an=![]() (n≥2),在①中令n=1得a1=2,
(n≥2),在①中令n=1得a1=2,
∴an=
(2)∵bn=![]() .
.
则当n=1时,S1=2
∴当n≥2时,Sn=2+2×2+3×22+…+n×2n﹣1
则2Sn=4+2×22+3×23+…+(n﹣1)2n﹣1+n2n
相减得Sn=n2n﹣(2+22+23+…+2n﹣1)=(n﹣1)2n+2(n≥2)
又S1=2,符合Sn的形式,
∴Sn=(n﹣1)2n+2(n∈N*)
-
科目: 来源: 题型:
查看答案和解析>>【题目】设{an}是首项为正数的等比数列,公比为q,则“q<0”是“对任意的正整数n,a2n﹣1+a2n<0”的条件.(填“充要条件、充分不必要条件、必要不充分条件、即不充分也不必要条件”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】设命题
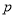 :
: 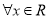 ,函数
,函数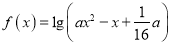 有意义;命题
有意义;命题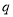 :
: 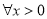 ,不等式
,不等式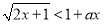 恒成立,如果命题“
恒成立,如果命题“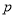 或
或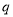 ”为真命题,命题“
”为真命题,命题“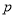 且
且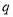 ”为假命题,求实数
”为假命题,求实数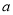 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若n=4时,则输出的结果为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}首项a1=2,前n项和为Sn , 且满足2an+1+Sn=3(n∈N*),则满足
 <
<  <
< 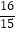 的所有n的和为 .
的所有n的和为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 (a>0且a≠1)在R上单调递减,且关于x的方程|f(x)|=2﹣x恰好有两个不相等的实数解,则a的取值范围是
(a>0且a≠1)在R上单调递减,且关于x的方程|f(x)|=2﹣x恰好有两个不相等的实数解,则a的取值范围是 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知动圆
 恒过点
恒过点 ,且与直线
,且与直线 :
:  相切.
相切.(1)求动圆圆心
 的轨迹
的轨迹 的方程;
的方程;(2)探究在曲线
 上,是否存在异于原点的两点
上,是否存在异于原点的两点 ,
,  ,当
,当 时,直线
时,直线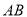 恒过定点?若存在,求出该定点坐标;若不存在,请说明理由.
恒过定点?若存在,求出该定点坐标;若不存在,请说明理由.
相关试题

