【题目】已知函数f(x)= ![]() (a>0且a≠1)在R上单调递减,且关于x的方程|f(x)|=2﹣x恰好有两个不相等的实数解,则a的取值范围是
(a>0且a≠1)在R上单调递减,且关于x的方程|f(x)|=2﹣x恰好有两个不相等的实数解,则a的取值范围是
参考答案:
【答案】[ ![]() ]∪{
]∪{ ![]() }
}
【解析】解:由y=loga(x+1)+1在[0,+∞) 上递减,得0<a<1,
又由f(x)= ![]() (a>0且a≠1)在R上单调递减,
(a>0且a≠1)在R上单调递减,
得02+3a≥f(0)=1,解得a ![]() ,
,
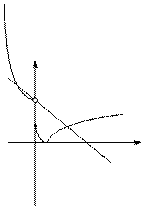
作出函数f(x)= ![]() (a>0且a≠1)在R上的大致图象,
(a>0且a≠1)在R上的大致图象,
由图象可知,在[0,+∞) 上,|f(x)|=2﹣x 有且仅有一个解,
故在(﹣∞,0)上,|f(x)|=2﹣x 同样有且仅有一个解,
当3a>2,即a> ![]() 时,联立|x2+3a|=2﹣x,
时,联立|x2+3a|=2﹣x,
则△=12﹣4(3a﹣2)=0,解得: ![]() ,
,
当1≤3a≤2 时,由图象可知,符合条件.
综上:a∈[ ![]() ]∪{
]∪{ ![]() }.
}.
所以答案是:[ ![]() ]∪{
]∪{ ![]() }.
}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若n=4时,则输出的结果为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】设数列
 满足:
满足:
 .
. (1)求数列
 的通项公式;
的通项公式;(2)设
 ,求数列
,求数列 的前
的前 项和
项和 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}首项a1=2,前n项和为Sn , 且满足2an+1+Sn=3(n∈N*),则满足
 <
<  <
< 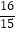 的所有n的和为 .
的所有n的和为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知动圆
 恒过点
恒过点 ,且与直线
,且与直线 :
:  相切.
相切.(1)求动圆圆心
 的轨迹
的轨迹 的方程;
的方程;(2)探究在曲线
 上,是否存在异于原点的两点
上,是否存在异于原点的两点 ,
,  ,当
,当 时,直线
时,直线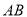 恒过定点?若存在,求出该定点坐标;若不存在,请说明理由.
恒过定点?若存在,求出该定点坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在以
 ,
,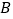 ,
,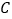 ,
,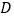 ,
,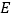 ,
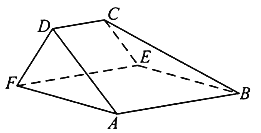
,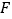 为顶点的五面体中,面
为顶点的五面体中,面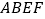 为正方形,
为正方形,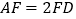 ,
,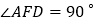 ,且二面角
,且二面角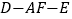 与二面角
与二面角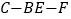 都是
都是 .
.
(1)证明:平面
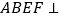 平面
平面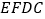 ;
;(2)求二面角
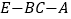 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C的对边分别是a,b,c,若
 +
+  =2a,b=
=2a,b=  ,则△ABC面积是
,则△ABC面积是
相关试题

