【题目】设数列{an}首项a1=2,前n项和为Sn , 且满足2an+1+Sn=3(n∈N*),则满足 ![]() <
< ![]() <
< ![]() 的所有n的和为 .
的所有n的和为 .
参考答案:
【答案】9
【解析】解:由2an+1+Sn=3(n∈N*),
∴2an+2+Sn+1=3,
两式相减得2an+2+Sn+1﹣2an+1﹣Sn=0,
即2an+2+an+1﹣2an+1=0,
则2an+2=an+1 ,
当n=1时,2a2+a1=3,
则a2= ![]() ,满足2a2=a1 ,
,满足2a2=a1 ,
即2an+1=an , 则 ![]() =
= ![]() ,即数列{an}是公比q=
,即数列{an}是公比q= ![]() ,首项a1=2的等比数列,
,首项a1=2的等比数列,
则数列{an}前n项和为Sn= ![]() =4﹣4(
=4﹣4( ![]() )n ,
)n ,
∴ ![]() =
= 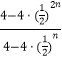 =1+(
=1+( ![]() )n ,
)n ,
∵ ![]() <
< ![]() <
< ![]() ,即
,即 ![]() <1+(
<1+( ![]() )n<
)n< ![]() ,
,![]() <(
<( ![]() )n<
)n< ![]() ,
,
则15<2n<33,
则n=4或5,
则4+5=9,
所以答案是:9.
【考点精析】通过灵活运用数列的前n项和,掌握数列{an}的前n项和sn与通项an的关系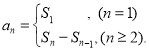 即可以解答此题.
即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设命题
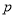 :
: 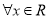 ,函数
,函数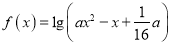 有意义;命题
有意义;命题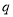 :
: 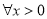 ,不等式
,不等式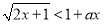 恒成立,如果命题“
恒成立,如果命题“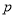 或
或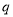 ”为真命题,命题“
”为真命题,命题“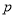 且
且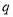 ”为假命题,求实数
”为假命题,求实数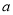 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若n=4时,则输出的结果为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】设数列
 满足:
满足:
 .
. (1)求数列
 的通项公式;
的通项公式;(2)设
 ,求数列
,求数列 的前
的前 项和
项和 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 (a>0且a≠1)在R上单调递减,且关于x的方程|f(x)|=2﹣x恰好有两个不相等的实数解,则a的取值范围是
(a>0且a≠1)在R上单调递减,且关于x的方程|f(x)|=2﹣x恰好有两个不相等的实数解,则a的取值范围是 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知动圆
 恒过点
恒过点 ,且与直线
,且与直线 :
:  相切.
相切.(1)求动圆圆心
 的轨迹
的轨迹 的方程;
的方程;(2)探究在曲线
 上,是否存在异于原点的两点
上,是否存在异于原点的两点 ,
,  ,当
,当 时,直线
时,直线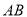 恒过定点?若存在,求出该定点坐标;若不存在,请说明理由.
恒过定点?若存在,求出该定点坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在以
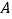 ,
,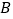 ,
,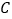 ,
,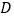 ,
,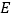 ,
,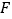 为顶点的五面体中,面
为顶点的五面体中,面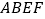 为正方形,
为正方形,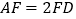 ,
,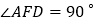 ,且二面角
,且二面角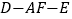 与二面角
与二面角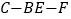 都是
都是 .
.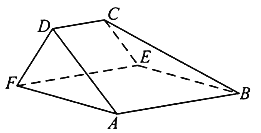
(1)证明:平面
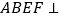 平面
平面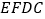 ;
;(2)求二面角
 的余弦值.
的余弦值.
相关试题

