【题目】已知函数f(x)=![]() +ax,aR,
+ax,aR,
(1)讨论函数f(x)的单调区间;
(2)求证:![]() ≥x;
≥x;
(3)求证:当a≥-2时,x[1,+ ∞),f(x)+lnx≥a+1恒成立.
参考答案:
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】试题分析:(1)由题意,求得![]() ,根据
,根据![]() 和
和![]() ,分类讨论,即可得到函数
,分类讨论,即可得到函数![]() 的单调区间;
的单调区间;
(2)令![]() ,由(1)可知,函数
,由(1)可知,函数![]() 的最小值为
的最小值为![]() ,即可证明不等式;
,即可证明不等式;
(3)不等式![]() 恒成立转化为不等式
恒成立转化为不等式![]() ,设出函数
,设出函数![]() ,利用导数求解函数
,利用导数求解函数![]() 的最小值,即可作出证明.
的最小值,即可作出证明.
试题解析:
(1)解:fˊ(x) = ![]() +a.
+a.
(i)当a≥0时, fˊ(x)>0,函数f(x)在R上单调递增;
(ii)当 a<0 时,令fˊ(x) =0,则ln(-a)+1,
当fˊ(x)>0,即x>ln( -a) + 1时,函数f (x)单调递增;
当fˊ(x)<0,即x<ln( -a) + 1时,函数f (x)单调递减.
综上,当a≥0时,函数f (x)在R上单调递增;当a<0时,函数f (x)的单调递增区间是(ln(-a)+1,+∞), 单调递减区间是(一∞,ln(-a)十1).
(2)证明:令 a= — 1,由(1)可知,函数/(x) =![]() —x 的最小值为f (1)=0,
—x 的最小值为f (1)=0,
∴![]() —x≥0, 即
—x≥0, 即![]() ≥x
≥x
(3)证明:f (x)十ln ≥a+1 恒成立与f (x)十ln x-a-1≥0 f恒成立等价.
令 g(x)=f(x)+lnx-a-1,g(x)=![]() + a(x—1)+ lnx-1,则gˊ(x) =
+ a(x—1)+ lnx-1,则gˊ(x) =![]() +
+![]() +a.
+a.
当a≥—2时,gˊ(x) = ![]() 十
十![]() 十a≥x十
十a≥x十![]() 十a≥
十a≥![]() +a = a十2≥0,(或令φ(x) =
+a = a十2≥0,(或令φ(x) = ![]() 十
十![]() ,则φˊx) =
,则φˊx) = ![]() —
—![]() 在[1,十∞)上递增,∴φˊ (x)在[1,十∞)上递增,∴φ(x) ≥φ(1) = 2,
在[1,十∞)上递增,∴φˊ (x)在[1,十∞)上递增,∴φ(x) ≥φ(1) = 2,
∴gˊ(x) ≥0).
∴g(x)在区间[1,十∞)上单调递增,
∴g(x) ≥g(1)=0,
∴ f(x)十ln x≥a+1 恒成立
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=Asin(ωx-
 )+1(A>0, ω>0)与ω=cosωx的部分图象如图所示。
)+1(A>0, ω>0)与ω=cosωx的部分图象如图所示。
(1)求A,a,b的值及函数f(x)的递增区间;
(2)若函数y= g(x-m)(m>
 )与y= f(x)+ f(x-
)与y= f(x)+ f(x-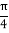 )的图象的对称轴完全相同,求m的最小值.
)的图象的对称轴完全相同,求m的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知经过原点的直线与椭圆
 交于
交于 两点,点
两点,点 为椭圆上不同于
为椭圆上不同于 的一点,直线
的一点,直线 的斜率均存在,且直线
的斜率均存在,且直线 的斜率之积为
的斜率之积为 .
.(1)求椭圆
 的离心率;
的离心率;(2)若
 ,设
,设 分别为椭圆的左、右焦点,斜率为
分别为椭圆的左、右焦点,斜率为 的直线
的直线 经过椭圆的右焦点,且与椭圆交于
经过椭圆的右焦点,且与椭圆交于 两点,若点
两点,若点 在以
在以 为直径的圆内部,求
为直径的圆内部,求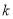 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某班一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,其中,频率分布直方图的分组区间分别为[50,60),[60,70),[70,80),[80,90),[90,100],据此解答如下问题.
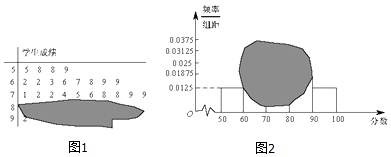
(Ⅰ)求全班人数及分数在[80,100]之间的频率;
(Ⅱ)现从分数在[80,100]之间的试卷中任取 3 份分析学生情况,设抽取的试卷分数在[90,100]的份数为X,求X的分布列和数学望期. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,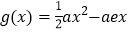 (
( ,
, 是自然对数的底数).
是自然对数的底数).(1)求函数
 的单调区间;
的单调区间;(2)若
 ,当
,当 时,求函数
时,求函数 的最大值;
的最大值;(3)若
 ,且
,且 ,比较:
,比较: 与
与 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
 中,
中,  .
.(Ⅰ)证明:
 ;
;(Ⅱ)平面

 平面
平面 ,
,  ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△
 内接于圆
内接于圆 ,
, 是圆
是圆 的直径,四边形
的直径,四边形 为平行四边形,
为平行四边形, 平面
平面 ,
, .
.
(1)求证:
 ⊥平面
⊥平面 ;
;(2)设
 ,
,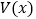 表示三棱锥
表示三棱锥 的体积,求函数
的体积,求函数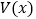 的解析式及最大值.
的解析式及最大值.
相关试题

