【题目】如图,△![]() 内接于圆
内接于圆![]() ,
,![]() 是圆
是圆![]() 的直径,四边形
的直径,四边形![]() 为平行四边形,
为平行四边形,![]() 平面
平面![]() ,
,![]() .
.

(1)求证:![]() ⊥平面
⊥平面![]() ;
;
(2)设![]() ,
,![]() 表示三棱锥
表示三棱锥![]() 的体积,求函数
的体积,求函数![]() 的解析式及最大值.
的解析式及最大值.
参考答案:
【答案】(1)见解析;(2)解析式见解析,最大值为3√3.
【解析】分析:(1)要证(1)要证![]() 平面
平面![]() ,需证
,需证![]() 平面
平面![]() ,需证
,需证![]() ,用综合法书写即可。
,用综合法书写即可。
(2)由(1)可知![]() 平面
平面![]() ,所以体积为
,所以体积为![]() ,
,![]() ,利用均值不等式求解最大值。
,利用均值不等式求解最大值。
详解:(1)证明:∵四边形DCBE为平行四边形,∴CD∥BE,BC∥DE.
∵DC⊥平面ABC,BC平面ABC,∴DC⊥BC.
∵AB是圆O的直径,∴BC⊥AC,且DC∩AC=C.
∴BC⊥平面ADC.
∵DE∥BC,∴DE⊥平面ADC;
(2)∵DC⊥平面ABC,∴BE⊥平面ABC.
在Rt△ABE中,AB=2,EB=3√.
在Rt△ABC中,∵AC=x,BC=4x2√(0<x<2).
∴S△ABC=12ACBC=12x4x2√,
∴V(x)=VEABC=3√6x4x2√,(0<x<2).
∵x2(4x2)(x2+4x22)2=4,当且仅当x2=4x2,即x=2√时,取等号,
∴x=2√时,体积有最大值为3√3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
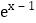 +ax,aR,
+ax,aR,(1)讨论函数f(x)的单调区间;
(2)求证:
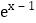 ≥x;
≥x;(3)求证:当a≥-2时,x[1,+ ∞),f(x)+lnx≥a+1恒成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,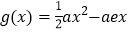 (
( ,
, 是自然对数的底数).
是自然对数的底数).(1)求函数
 的单调区间;
的单调区间;(2)若
 ,当
,当 时,求函数
时,求函数 的最大值;
的最大值;(3)若
 ,且
,且 ,比较:
,比较: 与
与 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
 中,
中,  .
.(Ⅰ)证明:
 ;
;(Ⅱ)平面

 平面
平面 ,
,  ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,若m<n,且f(m)=f(n),则n﹣m的取值范围是( )
,若m<n,且f(m)=f(n),则n﹣m的取值范围是( )
A.[3﹣2ln2,2)
B.[3﹣2ln2,2]
C.[e﹣1,2]
D.[e﹣1,2) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E,F分别为BC,AD的中点,点M在线段PD上. (Ⅰ)求证:EF⊥平面PAC;
(Ⅱ)如果直线ME与平面PBC所成的角和直线ME与平面ABCD所成的角相等,求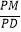 的值.
的值.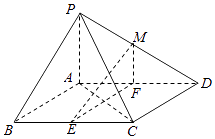
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,曲线Γ由曲线C1:
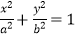 (a>b>0,y≤0)和曲线C2:
(a>b>0,y≤0)和曲线C2: 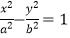 (a>0,b>0,y>0)组成,其中点F1 , F2为曲线C1所在圆锥曲线的焦点,点F3 , F4为曲线C2所在圆锥曲线的焦点,
(a>0,b>0,y>0)组成,其中点F1 , F2为曲线C1所在圆锥曲线的焦点,点F3 , F4为曲线C2所在圆锥曲线的焦点,
(Ⅰ)若F2(2,0),F3(﹣6,0),求曲线Γ的方程;
(Ⅱ)如图,作直线l平行于曲线C2的渐近线,交曲线C1于点A、B,求证:弦AB的中点M必在曲线C2的另一条渐近线上;
(Ⅲ)对于(Ⅰ)中的曲线Γ,若直线l1过点F4交曲线C1于点C、D,求△CDF1面积的最大值.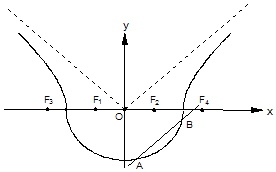
相关试题

